Following is a list of publications with preprints, lecture notes and demos, where applicable.
For the official research listing visit the Current Research Information System In Norway (Cristin).
Applications of Blending Splines in Interactive Geometric Modeling

University of Oslo. (2020).
Blending spline constructions are generated by blending local geometry using a smooth basis function. Compared with de facto industry standards used within CAGD, blending spline constructions are structurally complex. However, they enjoy a combined set of unique properties that are exploitable in real-world applications.
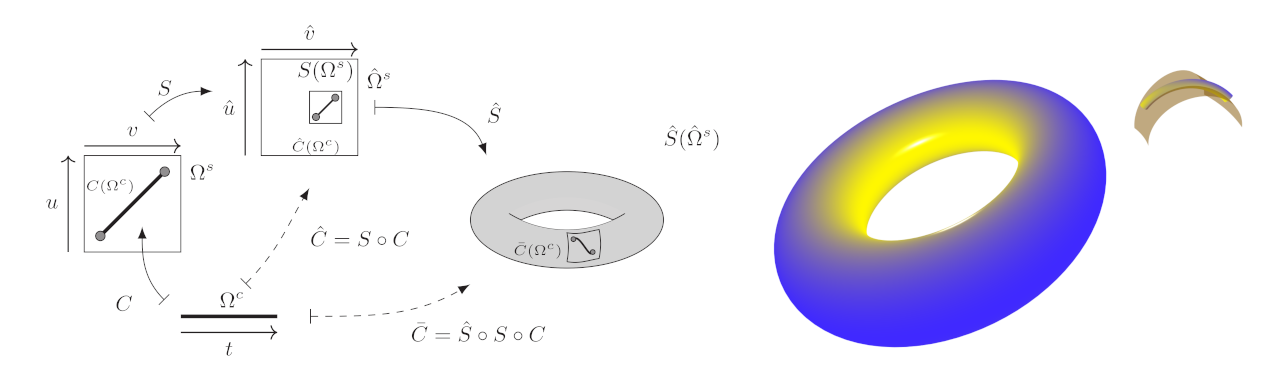
This ph.d. thesis investigates some of the construction's curve and surface applications in interactive geometric modeling (IGM). In particular, in the thesis's main contribution, the basis's property of vanishing derivatives is exploited to enable a patchwork interpretation for surface constructions. Together with a salient API feature of modern graphics hardware, this enables cost-consistent evaluation schemes. Moreover, the patchwork interpretation itself enables polygonal surface constructions with constant parameter lines that are non-dependent on the local surface type.
Software prototypes are utilized to develop and verify the thesis results. An in-house library built on a set of salient features of modern C++ is used for this purpose. With the thesis, a minimal feature version of this library is provided, and the feature utilization is argued.
Downloads: Bibtex
Exploring future C++ features within a geometric modeling context
In: NIK: Norsk Informatikkonferanse, vol. 2019 (2019).
The development of the C++ programming language and its standard library has undergone a renaissance since the emerge of the C++11 standard. Through modern features, expansions to the standard library and simplifications the language has become more relevant than ever before.
Comparing past and future feature sets (C++17, C++20, ...) is somewhat similar to comparing different programming languages. In this article we address how new and upcoming features of the language can be utilized to ease the development of domain specific application areas through features such as non-intrusive inheritance, semantic compiletime polymorphism and type safety.
We provide representative examples by application to differential geometry by modeling a hierarchical structure for parametric object evaluation.
Downloads: Bibtex
Evaluation of smooth spline blending surfaces using GPU
In: Curves and surfaces. 8th International Conference. Ed. by Jean-Daniel Boissonnat and Albert Cohen and Olivier Gibaru and Christian Gout and Tom Lyche and Marie-Laurence Mazure and Larry L. Schumaker, vol. 9213. Lecture Notes in Computer Science. Springer (2015), pp. 60 — 69.
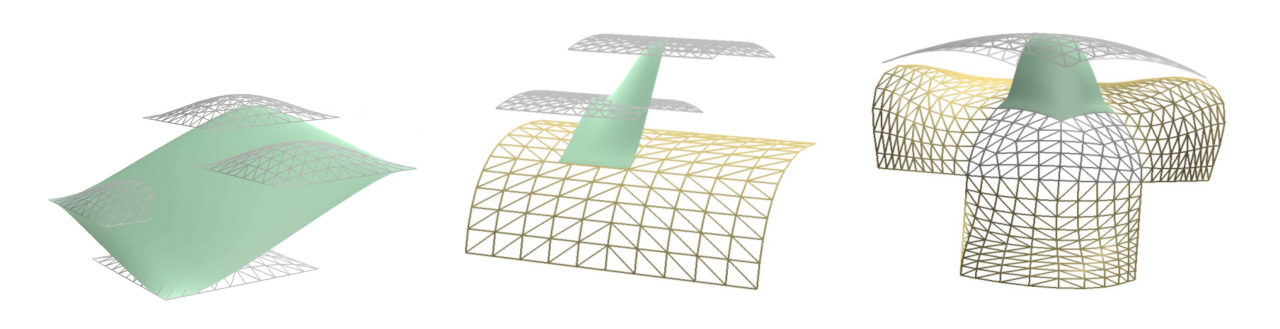
Recent development in several aspects of research on blending type spline constructions has opened up new application areas. We propose a method for evaluation and rendering of smooth blending type spline constructions using the tessellation shader steps of modern graphics hardware. In this preliminary study we focus on concepts and terminology rather than implementation details. Our approach could lead to more efficient, dynamic and stable blending-type spline based applications in fields such as interactive modeling, computer games and more.
Downloads: Bibtex
DOI: 10.1007/978-3-319-22804-4 launch
Spline representation of connected surfaces with custom-shaped holes
In: Large-Scale Scientific Computing 2015. Ed. by Ivan Lirkov and Svetozar Margenov and Jerzy Waśniewski, vol. 9374. Lecture Notes in Computer Science. Springer (2015), pp. 394 — 400.
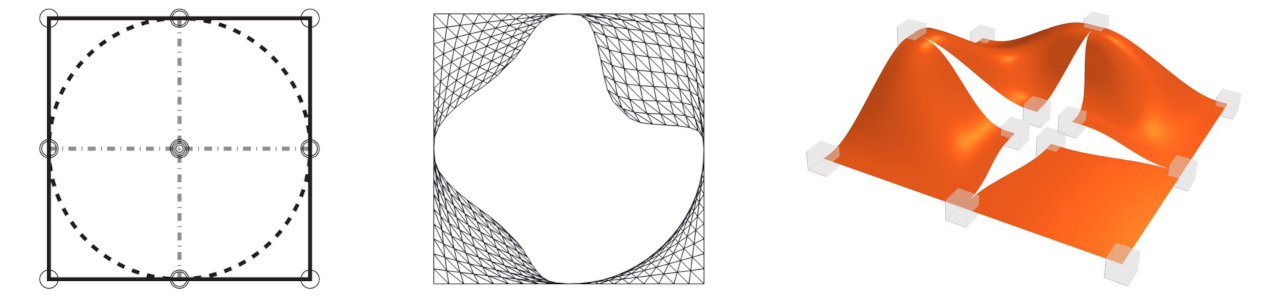
Compact surfaces possessing a finite number of boundaries are important to isogeometric analysis (IGA). Generalized expo-rational B-Splines (GERBS) is a blending type spline construction where local functions associated with each knot are blended by Ck-smooth basis functions. Modeling of surfaces with custom-shaped boundaries, or holes, can be achieved by using certain features and properties of the blending type spline construction, including local refinement and insertion of multiple inner knots. In this paper we investigate representation of arbitrary inner boundaries on parametric surfaces by using the above mentioned blending type spline construction.
Downloads: Bibtex
DOI: 10.1007/978-3-319-26520-9_44 launch
Image compression using an adjustable basis function

In: Mathematics in Engineering, Science and Aerospace, vol. 6, no. 1 (2015), pp. 25 — 34.
We investigate the performance of image compression using a custom transform, related to the discrete cosine transform, where the shape of the waveform basis function can be adjusted via setting a shape parameter. A strategy for generating quantization tables for various shapes of the basis function, including the cosine function, is proposed. Two signal fidelity measures, peak signal-tonoise ratio and mean structural similarity index, respectively, are computed for a few selected photos to benchmark the results.
Downloads: Bibtex
Wavelet compression of spline coefficients
In: Numerical Methods and Applications 2014. Ed. by Ivan Dimov and Stefka Fidanova and Ivan Lirkov, vol. 8962. Lecture Notes in Computer Science. Springer (2015), pp. 246 — 253.
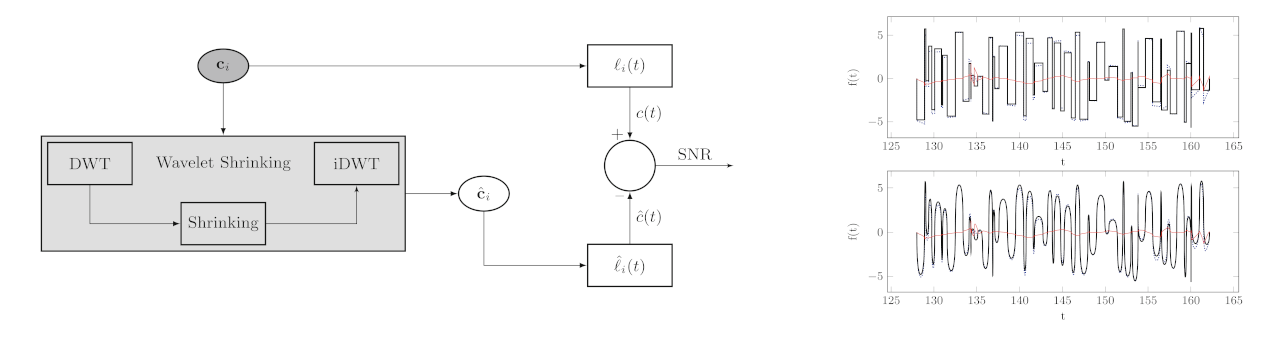
Based on a concept for thresholding of wavelet coefficients, which was addressed in [8] and further explored in [6, 7], a method for balancing between non-threshold- and threshold shrinking of wavelet coefficients has emerged. Generalized expo-rational B-splines (GERBS) is a blending type spline construction where local functions at each knot are blended together by Ck-smooth basis functions. Global data fitting can be achieved with GERBS by fitting local functions to the data. One property of the GERBS construction is an intrinsic partitioning of the global data. Compression of the global data set can be achieved by applying the shrinking strategy to the GERBS local functions. In this initial study we investigate how this affects the resulting GERBS geometry.
Downloads: Bibtex
DOI: 10.1007/978-3-319-15585-2_27 launch
Performance of a wavelet shrinking method
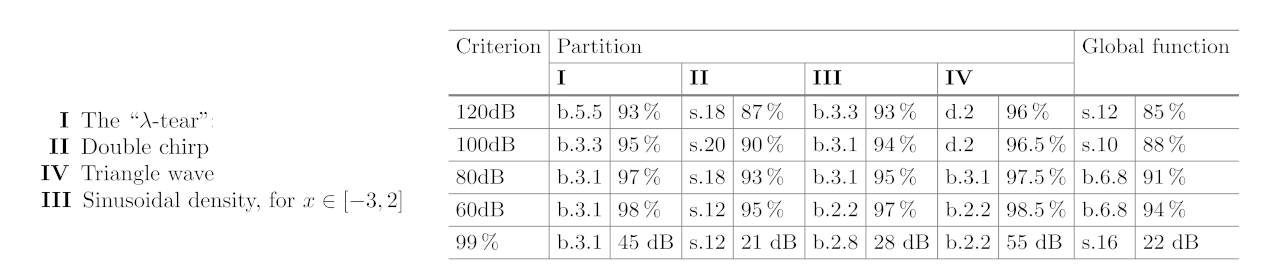
In: Numerical Methods and Applications 2014. Ed. by Ivan Dimov and Stefka Fidanova and Ivan Lirkov, vol. 8962. Lecture Notes in Computer Science. Springer (2015), pp. 262 — 270.
A concept for shrinking of wavelet coefficients has been presented and explored in a series of articles [2–4]. The theory and experiments so far suggest a strategy where the shrinking adapts to local smoothness properties of the original signal. From this strategy we employ partitioning of the global signal and local shrinking under smoothness constraints. Furthermore, we benchmark shrinking of local partitions’ wavelet coefficients utilizing a selection of wavelet basis functions. Then we present and benchmark an adaptive partition-based shrinking strategy where the best performing shrinkage is applied to individual partitions, one at a time. Finally, we compare the local and global benchmark results.
Downloads: Bibtex
DOI: 10.1007/978-3-319-15585-2_29 launch
Motion capture data represented using a blending type spline construction
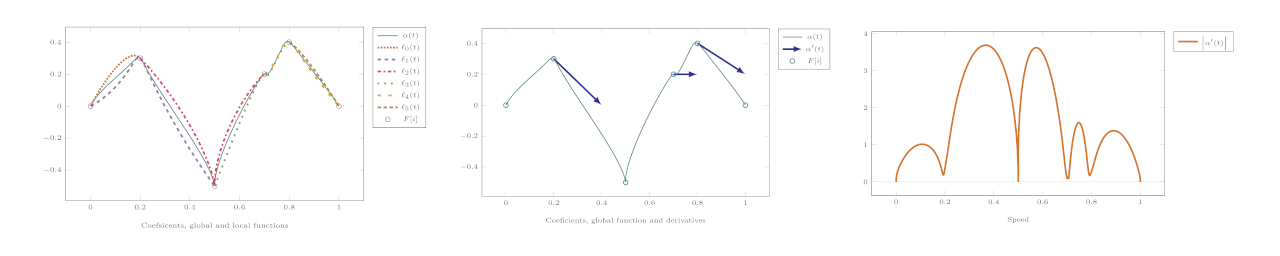
In: 40th International conference applications of mathematics in engineering and economics AMEE14. Ed. by Vesela Pasheva and George Venkov, vol. 1631. AIP Conference Proceedings. AIP Publishing (2014), pp. 153 — 157.
We present a concept for representation of motion-capture data where information from the animation data is used to generate a blending-type spline curve using local curves of Hermite type
Downloads: Bibtex
DOI: 10.1063/1.4902471 launch
Data approximation using a blending type spline construction
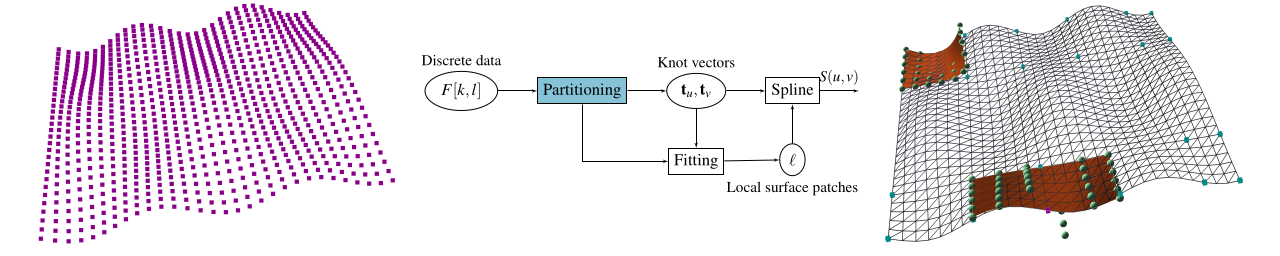
In: 40th International conference applications of mathematics in engineering and economics AMEE14. Ed. by Vesela Pasheva and George Venkov, vol. 1631. AIP Conference Proceedings. AIP Publishing (2014), pp. 147 — 152.
Generalized expo-rational B-splines (GERBS) is a blending type spline construction where local functions at each knot are blended together by Ck-smooth basis functions. One way of approximating discrete regular data using GERBS is by partitioning the data set into subsets and fit a local function to each subset. Partitioning and fitting strategies can be devised such that important or interesting data points are interpolated in order to preserve certain features. We present a method for fitting discrete data using a tensor product GERBS construction. The method is based on detection of feature points using differential geometry. Derivatives, which are necessary for feature point detection and used to construct local surface patches, are approximated from the discrete data using finite differences.
Downloads: Bibtex
DOI: 10.1063/1.4902470 launch
Image processing with LERBS
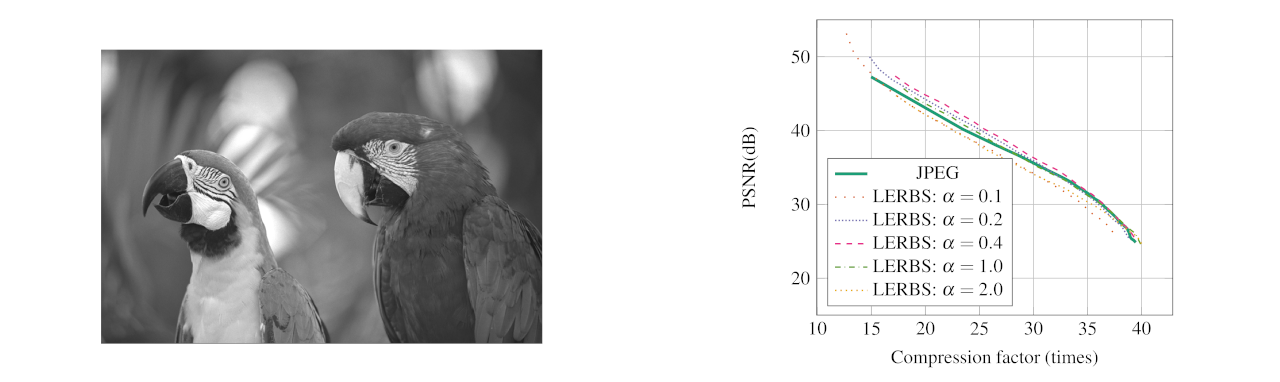
In: ICNPAA 2014 World Congress: 10th International conference on Mathematical Problems in Engineering, Aerospace and Sciences. Ed. by Seenith Sivasundaram, vol. 1637. AIP Conference Proceedings. AIP Publishing (2014), pp. 271 — 278.
We investigate the performance of image compression using a custom transform, related to the discrete cosine transform, where the shape of the waveform basis function can be adjusted via setting a shape parameter. A strategy for generating quantization tables for various shapes of the basis function, including the cosine function, is proposed.
Downloads: Bibtex
DOI: 10.1063/1.4904588 launch
Surface deformation over flexible joints using spline blending techniques
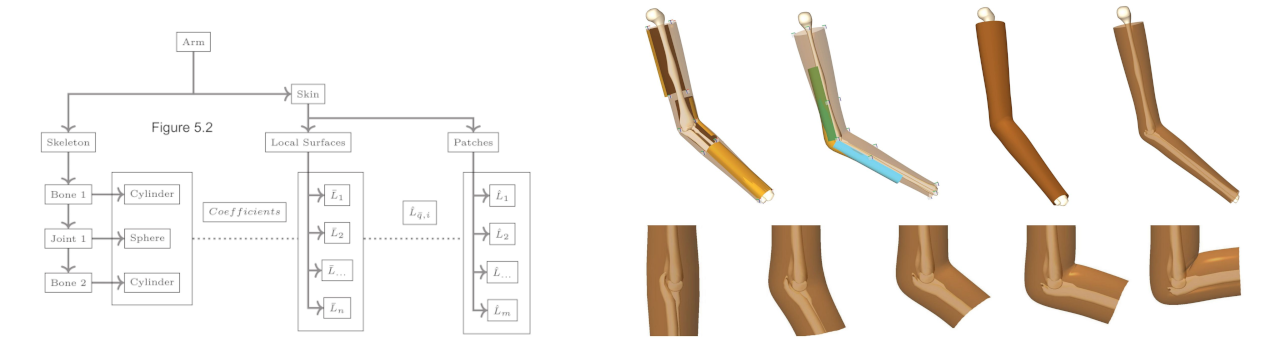
In: ICNPAA 2014 World Congress: 10th International conference on Mathematical Problems in Engineering, Aerospace and Sciences. Ed. by Seenith Sivasundaram, vol. 1637. AIP Conference Proceedings. AIP Publishing (2014), pp. 377 — 383.
Skinning over a skeleton joint is the process of skin deformation based on joint transformation. Popular geometric skinning techniques include implicit linear blending and dual quaternions. Generalized expo-rational B-splines (GERBS) is a blending type spline construction where local functions at each knot are blended by Ck-smooth basis functions. A smooth skinning surface can be constructed over a transformable skeleton joint by combining various types of local surface constructions and applying local Hermite interpolation. Compared to traditional spline methods, increased flexibility and local control with respect to surface deformation can be achieved using the GERBS blending construction. We present a method using a blending-type spline surface for skinning over a flexible joint, where local geometry is individually adapted to achieve natural skin deformation based on skeleton transformations..
Downloads: Bibtex
DOI: 10.1063/1.4904602 launch
Smooth spline blending surface approximation over a triangulated irregular network

In: International Journal of Applied Mathematics, vol. 27, no. 1 (2014), pp. 109 — 119.
A Triangulated Irregular Network (TIN) is a data structure commonly used to represent a geometric surface in computer software systems, such as geographic information systems and terrain modeling systems. Exporational B-splines (ERBS), a blending type spline construction in the family of generalized expo-rational B-splines (GERBS), can be used to create an approximation surface which interpolates the vertex positions of the TIN nodes. Utilizing the properties for local support of this blending spline construction, one can construct an approximation surface which is local within the second neighbourhood with respect to the infliction nodes of the underlying TIN. We present two variations of blending functions used with the construction. The first one blends the TIN edges with a smooth component, thus, the surface approximation is only C0 over the TIN edges. The second blending method provides a surface approximation which is smooth over the TIN edges.
Downloads: Bibtex
Fitting of Discrete Data with GERBS
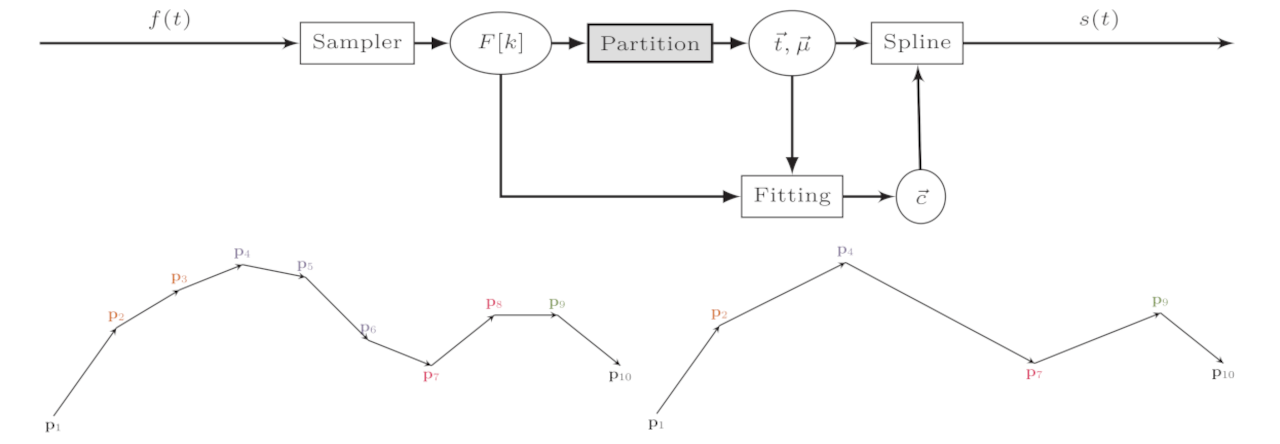
In: Large-Scale Scientific Computing 2013. Ed. by Ivan Lirkov and Svetozar Margenov and Jerzy Waśniewski, vol. 8353. Lecture Notes in Computer Science. Springer (2014), pp. 569 — 576.
In this paper, we present a study of fitting discrete data with Generalized Expo-rational B-splines. We investigate different ways to determine interpolation knots and generate GERBS local curves by partitioning the parametric space and solving a corresponding least-squares fitting problem. We apply our technique to discrete evaluations of continuous synthetic benchmark functions and compare the resulting GERBS to the original data with respect to errors and performance.
Downloads: Bibtex
DOI: 10.1007/978-3-662-43880-0_66 launch
Discrete Wavelet Compression of ERBS

In: Large-Scale Scientific Computing 2013. Ed. by Ivan Lirkov and Svetozar Margenov and Jerzy Waśniewski, vol. 8353. Lecture Notes in Computer Science. Springer (2014), pp. 577 — 584.
We study the application of Lorentz thresholding and composite Besov-Lorentz shrinkage to coefficients of wavelet-transformed discretized expo-rational B-spline (ERBS) data. ERBS constructions are well suited for interpolation in cases where a given continuity is required; including, but not limited to, applications within control theory, simulations and various interactive modeling. We provide different examples, which highlight the adaptivity features of the two methods. We show the performance with respect to compression rates and approximation errors for the two test cases.
Downloads: Bibtex
DOI: 10.1007/978-3-662-43880-0_67 launch
Local refinement of GERBS surfaces with applications to interactive geometric modeling

In: 39th International conference applications of mathematics in engineering and economics AMEE13. Ed. by Vesela Pasheva and George Venkov, vol. 1570. AIP Conference Proceedings. AIP Publishing (2013), pp. 18 — 25.
Generalised Expo-rational B-splines (GERBS) is a blending type spline construction, which blends local functions with up to Ck-smoothness. The GERBS blending construction combined with an ERBS basis (ERBS curve, ERBS surface, etc.) blends local functions with infinite smoothness. The ERBS blending construction was created specially with free form interactive geometric modelling in mind. One of the intrinsic properties of the GERBS bases used in the blending construction is the minimal support of the basis functions, which facilitates local editing. In this work we look at local refinement of GERBS tensor product surfaces and constructions which could enhance the dynamic editing capabilities of the GERBS construction. We investigate knot insertion on GERBS and then introducing a method for local refinement with the use of blending. With the aim of preserving local support.
Downloads: Bibtex
DOI: 10.1063/1.4854738 launch
Index Mapping between Tensor-Product Wavelet Bases of Different Number of Variables, and Computing Multivariate Orthogonal Discrete Wavelet Transforms on Graphics Processing Units
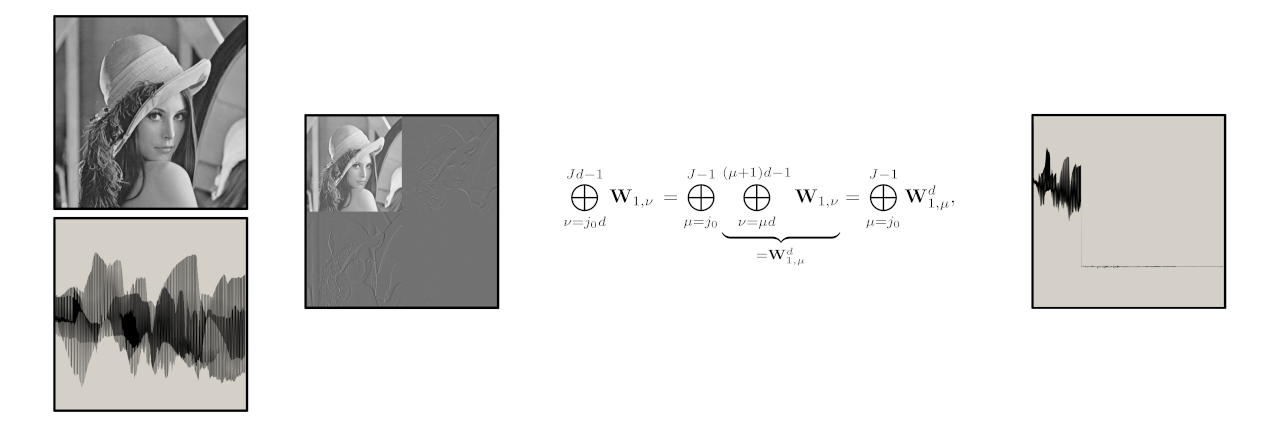
In: Large-Scale Scientific Computing 2011. Ed. by Ivan Lirkov and Svetozar Margenov and Jerzy Waśniewski, vol. 7116. Lecture Notes in Computer Science. Springer (2012), pp. 402 — 410.
An algorithm for computation of multivariate wavelet transforms on graphics processing units (GPUs) was proposed in [1]. This algorithm was based on the so-called isometric conversion between dimension and resolution (see [2] and the references therein) achieved by mapping the indices of orthonormal tensor-product wavelet bases of different number of variables and a tradeoff between the number of variables versus the resolution level, so that the resulting wavelet bases of different number of variables are with different resolution, but the overall dimension of the bases is the same.
In [1] we developed the algorithm only up to mapping of the indices of blocks of wavelet basis functions. This was sufficient to prove the consistency of the algorithm, but not enough for the mapping of the individual basis functions in the bases needed for a programming implementation of the algorithm. In the present paper we elaborate the full details of this ‘book-keeping’ construction by passing from block-matrix index mapping on to the detailed index mapping of the individual basis functions. We also consider some examples computed using the new detailed index mapping.
Downloads: Bibtex
DOI: 10.1007/978-3-642-29843-1_45 launch
Wavelet-based lossless one- and two-dimensional representation of multidimensional geometric data
In: 37th International conference applications of mathematics in engineering and economics AMEE11, vol. 1410, no. 1. AIP Publishing (2011), pp. 83 — 97.
In the present communication we develop a complete representation of whole multidimensional manifolds, with the Cantor diagonal type of algorithm [1, 2] replaced by a new and simpler type of Cartesian‐indexing basis‐matching algorithm [3]. We provide graphical comparison between the results obtained via the Cantor diagonal algorithm and the Cartesian‐indexing algorithm. For this purpose, we test the algorithms on several different types of ‘benchmark’ multidimensional manifolds: Green's functions for linear PDEs, Cartesian products of 3‐dimensional manifolds, intersections of multidimensional manifolds. One new type of intersection problems which can be solved invoking the new representation is computing the intersections of multidimensional manifolds in parametric form (rather than only in implicit form, as earlier [3]).
This work is based on research conducted within two consecutive Strategic Projects of the Norwegian Research Council: ‘GPGPU—Graphics Hardware as a High‐end Computational Resource’ (2004‐2007) and ‘Heterogeneous Computing’ (2008‐2010).
Downloads: Bibtex
DOI:
10.1063/1.3664359
launch
ISBN: 978-0-7354-0984-2
Methods for userguided compression algorithms
In: NIK: Norsk Informatikkonferanse, vol. 2011 (2011), pp. 259 — 262.
In computer games of today and specially massively multiplayer online role playing games virtual world and the characters therein are becoming more and more realistic, and therefore demands a larger and larger amount of data to be described in detail. As a part of the ’DreamWorld’ research project, Funcom and Narvik University College have entered into a co-operation to find new ways to handle some of the issues linked to this.
This paper gives and introduction to a PhD project which aim is to develop new methods for user guided compression algorithms. It also aims to end up with a prototype for a user guided animation-compression-tool for seamless integration into an already existing production pipeline.
Downloads: Bibtex