
C++ Diferential Geometry Prototyping
I started the development of GMlib2 while working on a prototyping software for the Blending Spline Polygon article, published as part of my thesis read_more . The construction utlized many layers of geometric sub-object constructions, and we wanted the prototyping software to provide this feature in a automatic and deductive manner. Therefor, the main motivation for the library was to utilize modern C++ and compiler features to enforce consistensy and reduce constructional errors.
Some thoughts regarding the design and C++ features was published in NIK 2019, read_more , and presented at the NIK konference in Narvik in 2019. Aside from GMlib2, which lives its own life, a toy concept library containing the examples from the paper and presentation at NIK, was also published. A link to the library can be found at the bottom.
This project post describes the C++ building blocks and techniques from the NIK 2019 presentation, together with a set of toy library examples, and rendered graphics from GMlib2. We'll start by exploring the utliized key C++ modeling techniques,
- Non-intrusive inheritance;
- Semantic compile-time polymorphism;
- Aggregate properties; and
- Transitive constructors and member functions.
Motivation
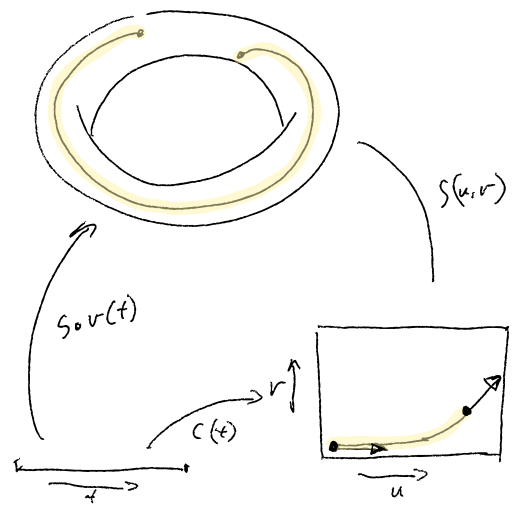
Let us argue the motivation through a couple of exampls. The two examples below shows sketches of constructions, as usually dreamt up on a whiteboard, and what they look like rendered on a computer.
The first example shows a Hermite curve (1D cuve) embedded in a plane (2D surface) which again is embedded in a Torus (surface).
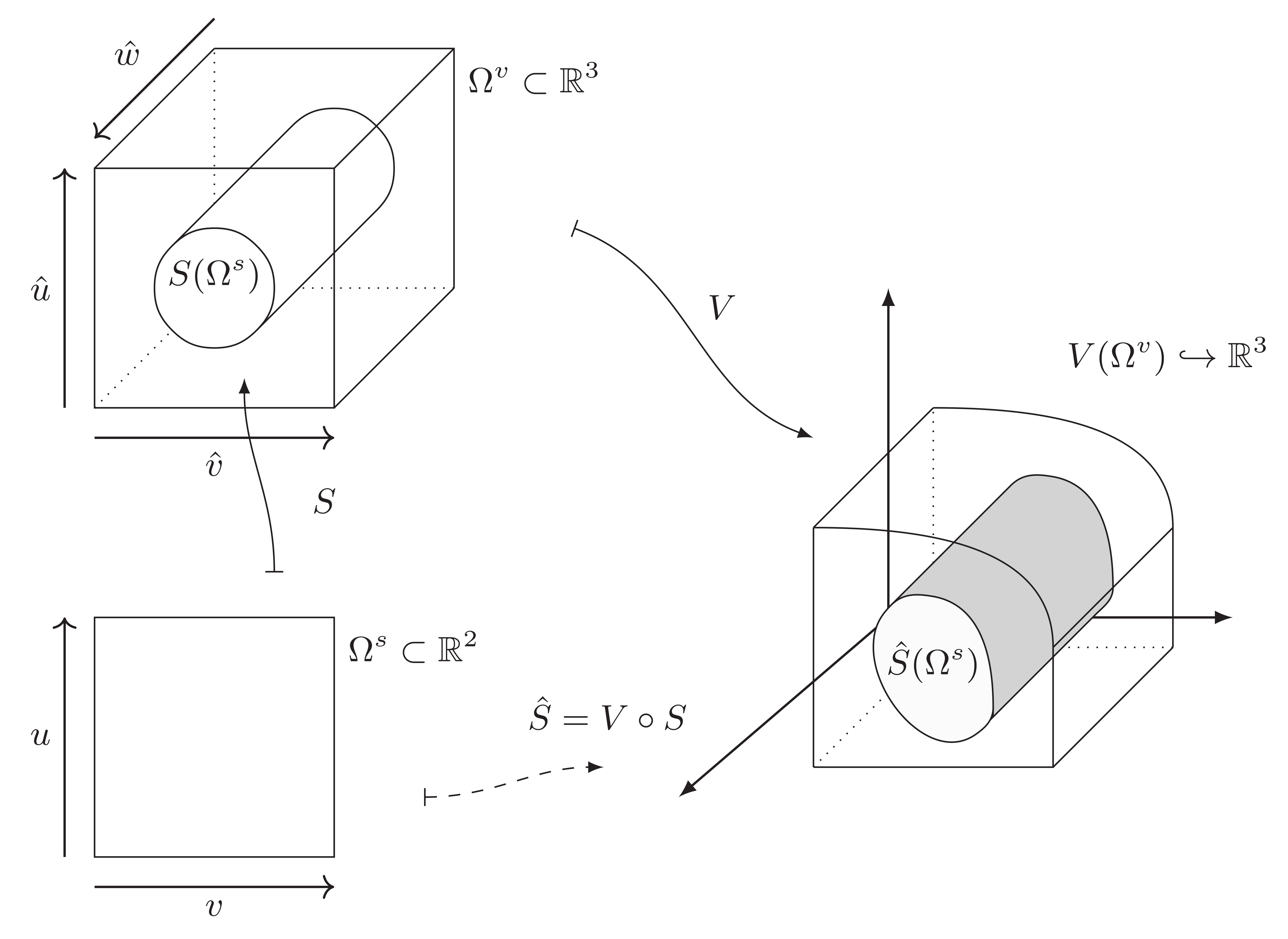
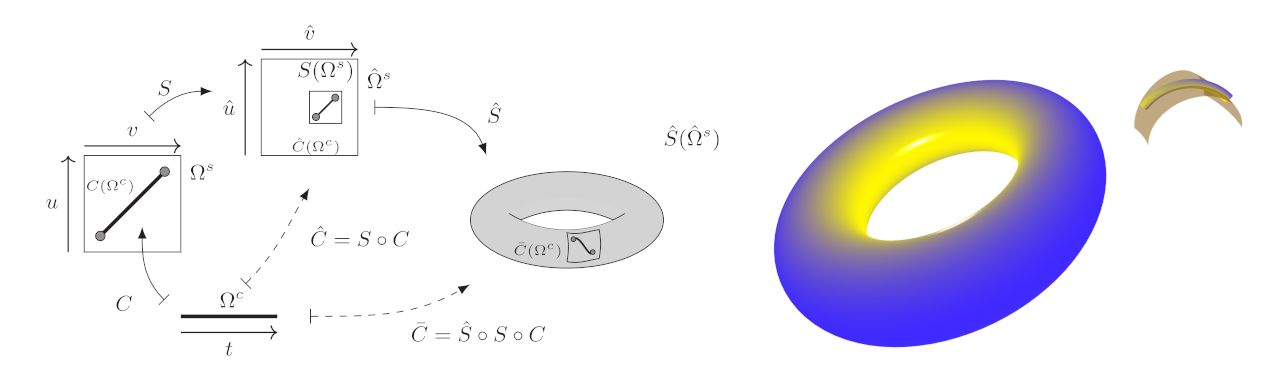 In another example we see a cylinder (surface) embedded in a Bezier-volume (3D volume).
In another example we see a cylinder (surface) embedded in a Bezier-volume (3D volume).

|
As a usage example, where the internal cylinder is naturally embedded in the Bezier volume, the cylinder will be transformed upon transforming the Bezier-volume as the internal parametric space of the Bezier volume is compressed or expanded.


These constructions naturally presents us with a set of co-dependent data. We wanted to propagate this data through our construction. In addition our internal tools were based in C++ and with the emergence of modern C++ we wanted to move as much of the constructional static data into the static space of constructions, so that we could enable compiler usage to validate our constructions. We therefor desided to build a template-based generic library for this purpose.
Principal design techniques
Non-intrusive inheritance
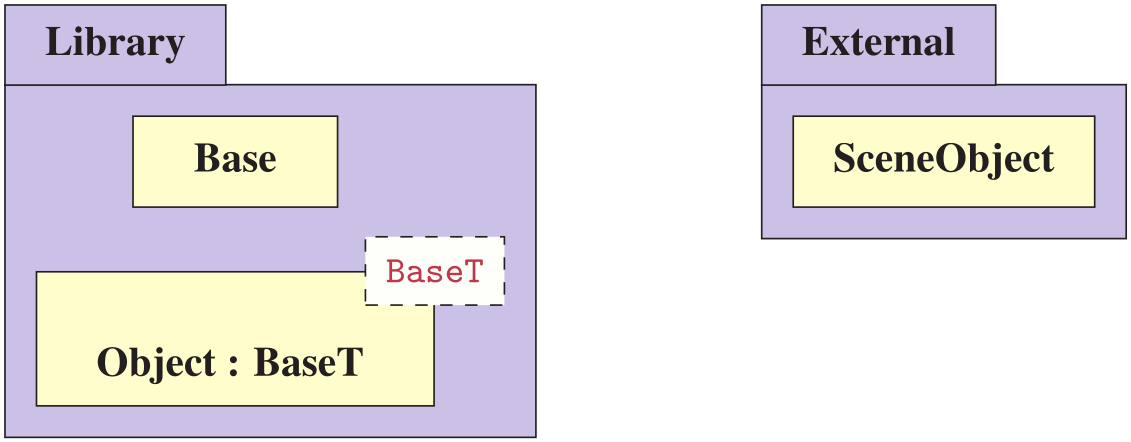
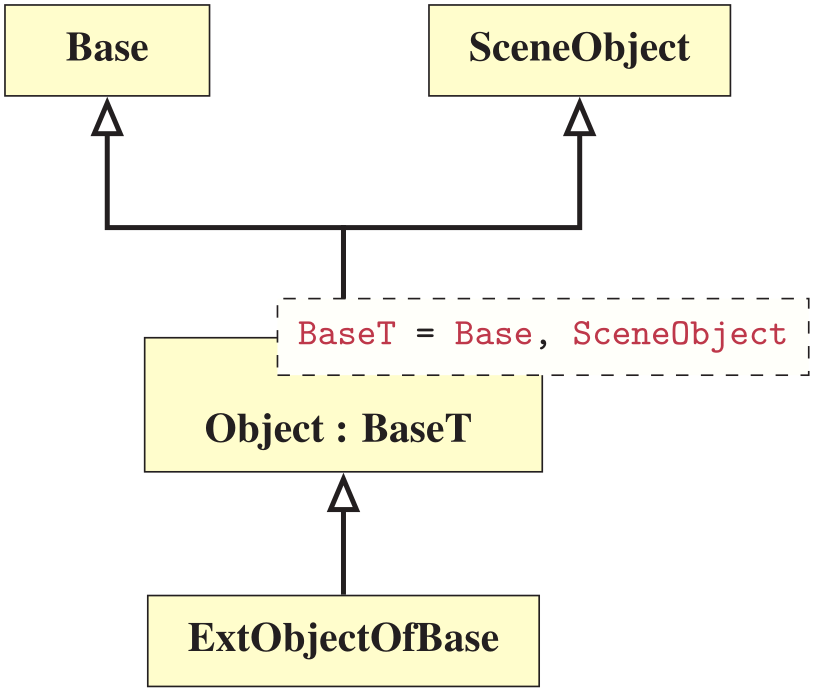
The term non-intrusive inheritance refers to an inheritance model where a derived class can inherit a realized base class, possibly unknown at the time of design, where the realized base class adheres to a set of static rules such that the memory model is preserved at the time of compilation. For instance, the derived class is defined in a library, but the realized base class can be designed by the library's end-user.
|
To facilitate non-intrusive inheritance one can utilize variadic class templates;
{template ⟨typename... Ts⟩}{...}
// Library
struct Base {};
template ⟨typename... Base_Ts⟩
struct Object : Base_Ts... {};
// External Library
struct ExtObject {};
// Application code
using NonInheritingObject = Object<>;
using ExtObjectOfBase = Object⟨ExtObject,Base⟩;
Semantic compile-time polymorphism
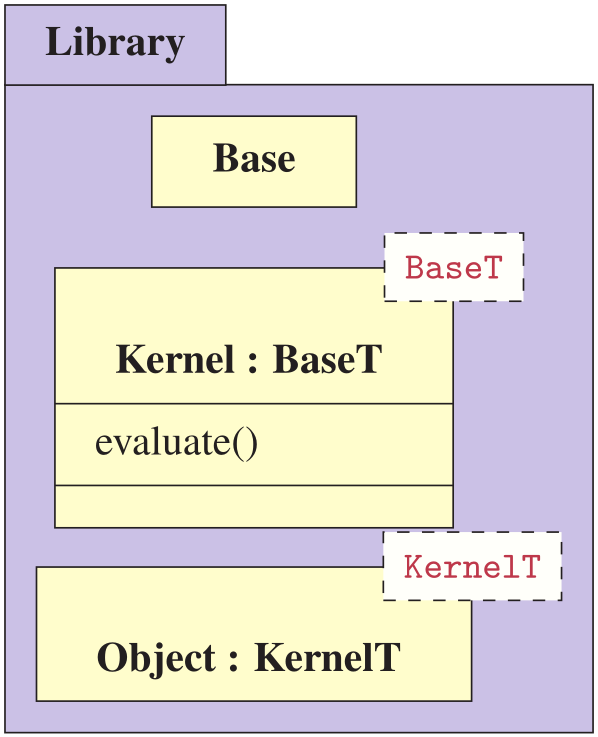
The standard mechanisms used in C++ to implement polymorphism are function overloading and virtual functions. The latter enables runtime-dynamic types where the semantics of a derived object can be reimplemented for a given virtual function in a derived class and then be called for the derived object dynamically through a pointer of the base class type.
|
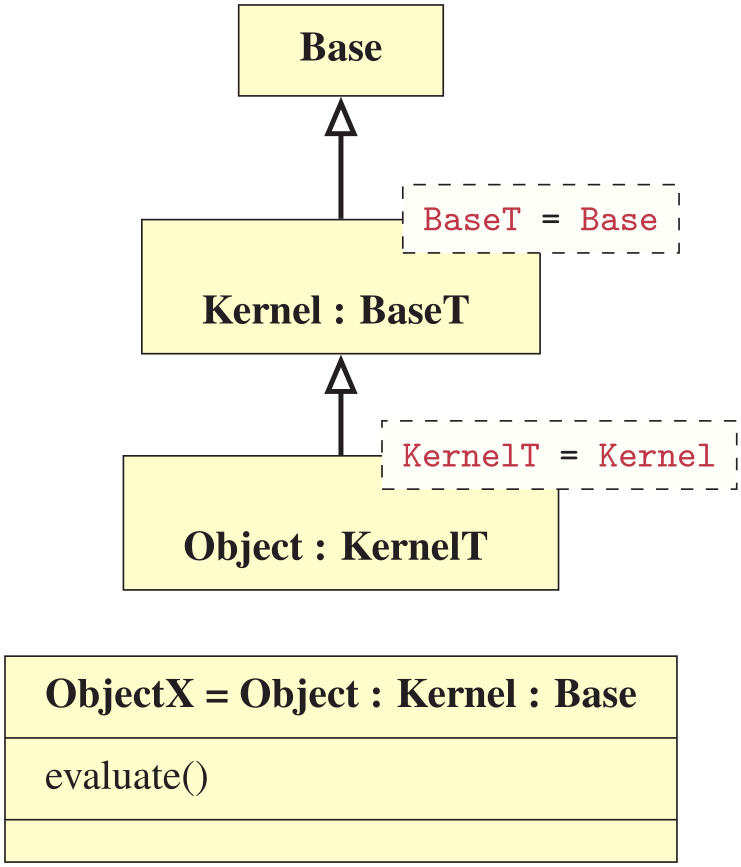
By flattening the structure, using a middle layer kernel type, utilizing non-intrusive inheritance, and exploiting function overloading, we can mimic much of the same behaviour for semantic compile-time polymorphism.
Let us look at an example
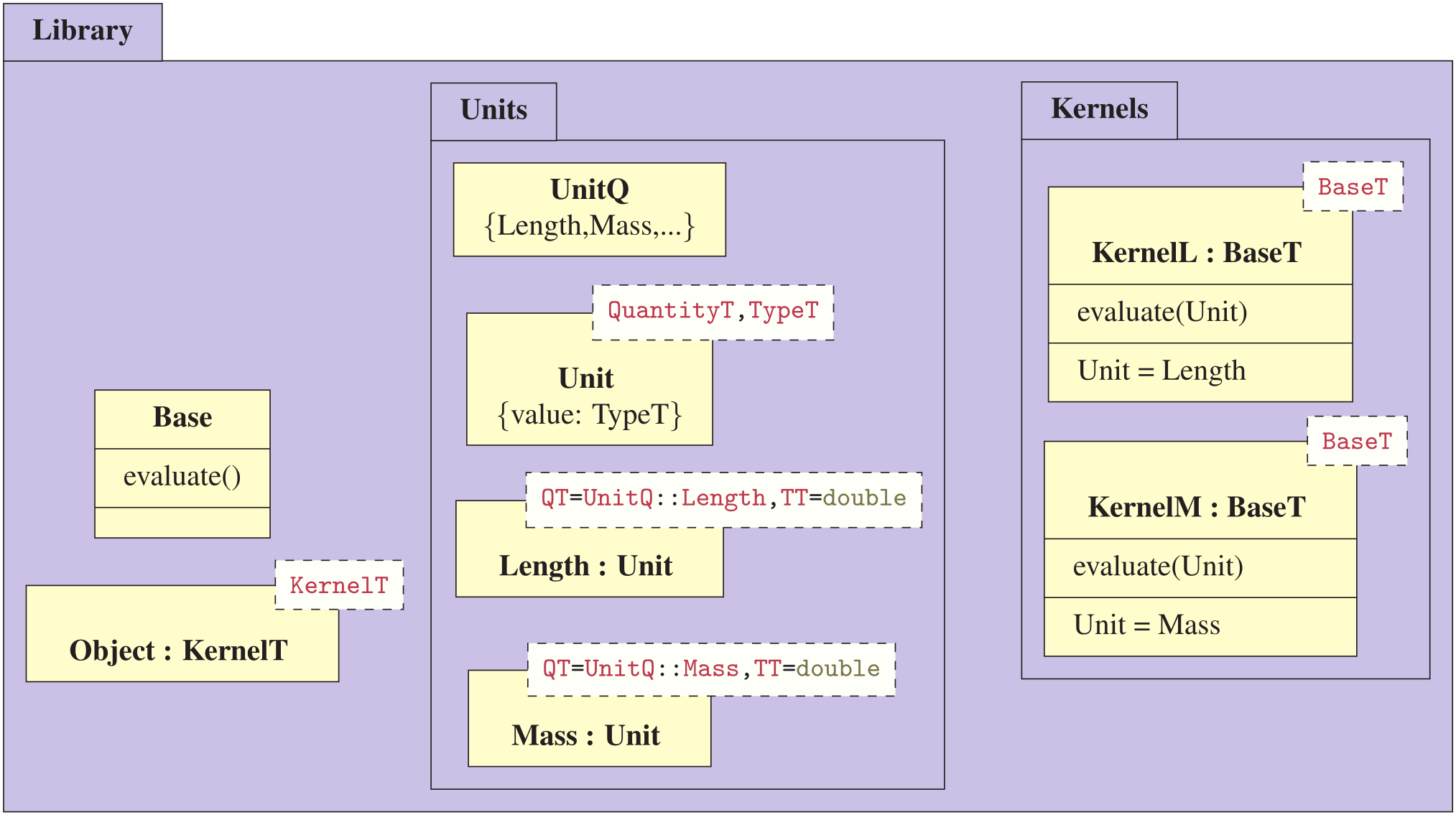
Consider the following library;
|
expressed in code as follows:
template ⟨int Q_m, int Q_kg⟩
struct UnitQ { enum {Length = Q_m, Mass = Q_kg}; };
template ⟨typename /*UnitQ_T*/, typename Type_T = double⟩
struct Unit { Type_T value; };
using Length = Unit⟨UnitQ<1,0>⟩;
using Mass = Unit⟨UnitQ<0,1>⟩;
struct Base {};
⟨typename Kernel_T⟩
struct Object : Kernel_T {};
template ⟨Base_T⟩
struct KernelL : Base_T {
auto evaluate( Length l ) { return l; }
auto evaluate() { return double(0.5); } };
template ⟨Base_T⟩
struct KernelM : Base_T {
auto evaluate( Mass m ) { return m; }
auto evaluate() { return double(0.5); } };
template ⟨typename Obj_T, typename... Params_Ts⟩
auto evaluate(Obj_T t, Param_Ts... params){
return t.evaluate(std::forward⟨Ts⟩(params)...); }
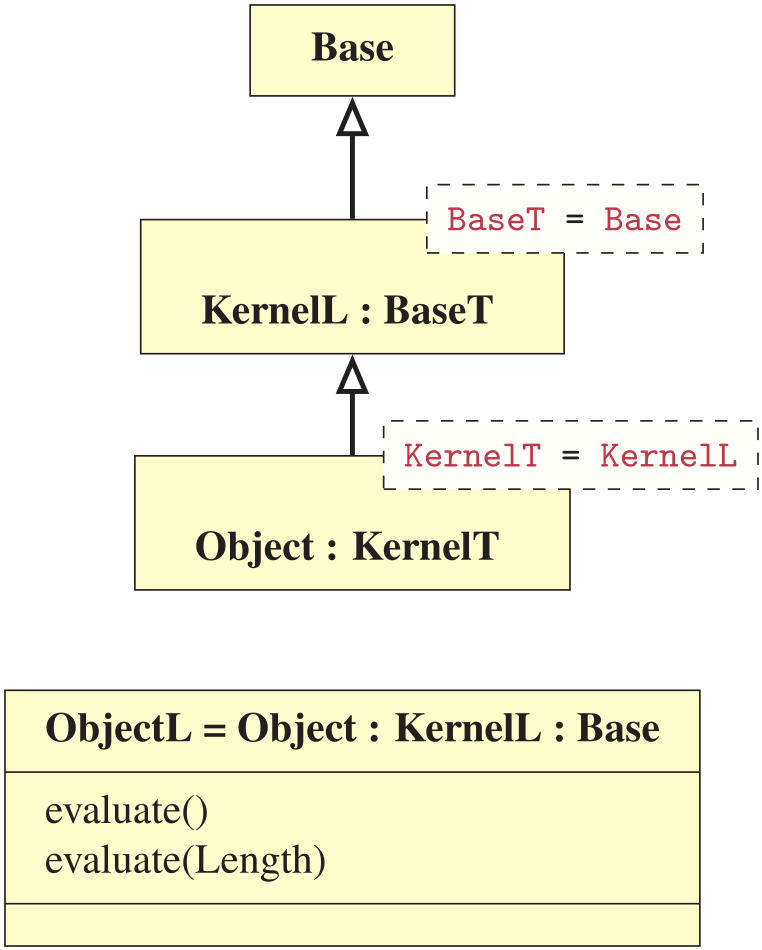
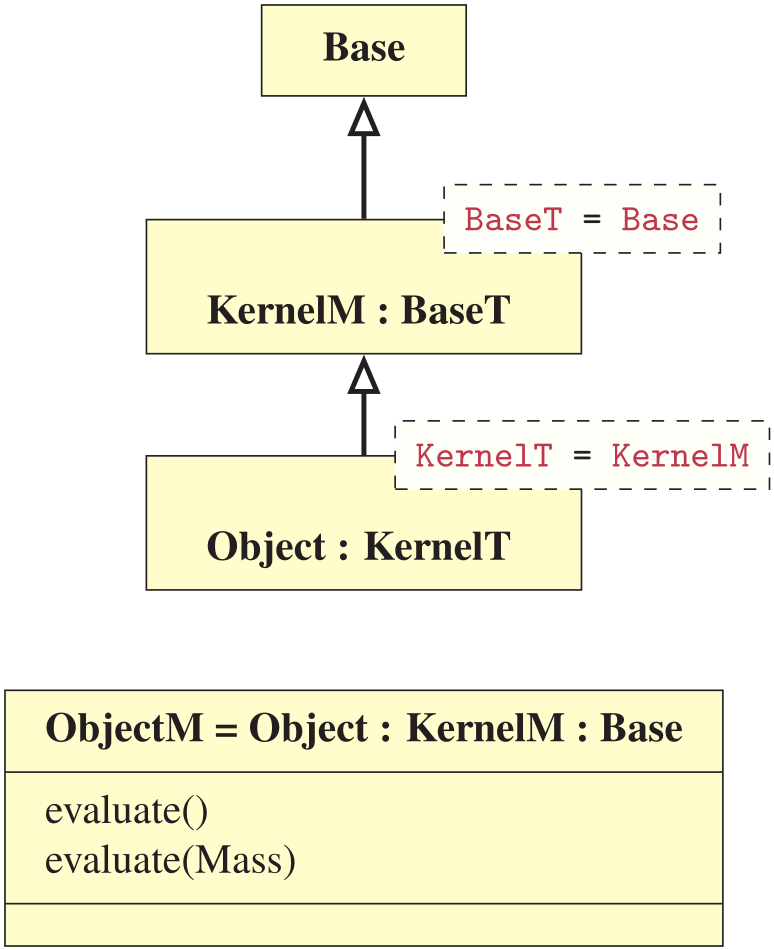
The Object class inherits a potential kernel which again inherits a common base.
using ObjectL = Object⟨ KernelL⟨ Base ⟩ ⟩;
using ObjectM = Object⟨ KernelM⟨ Base ⟩ ⟩;
|
The defined objects ObjectL and ObjectM share the same polymorphic API, where the return type is deduced by binding to the unconstrained placeholder type auto. Both object types can then be utilized in polymorphic contexts, as follows:
auto L = ObjectL;
auto M = ObjectM;
auto a = evaluate(L, Length{4.}); // Ok
auto a = evaluate(L, 4.); // Ok
auto b = evaluate(M); // Ok
auto c = evaluate(L, Mass{4.}); // Compile error: parameter type mismatch
int d = evaluate(L, 4.); // Compile error: return type mismatch in assignment
auto e = evaluate(M, 4); // Compile error: parameter type mismatch
Aggregated properties
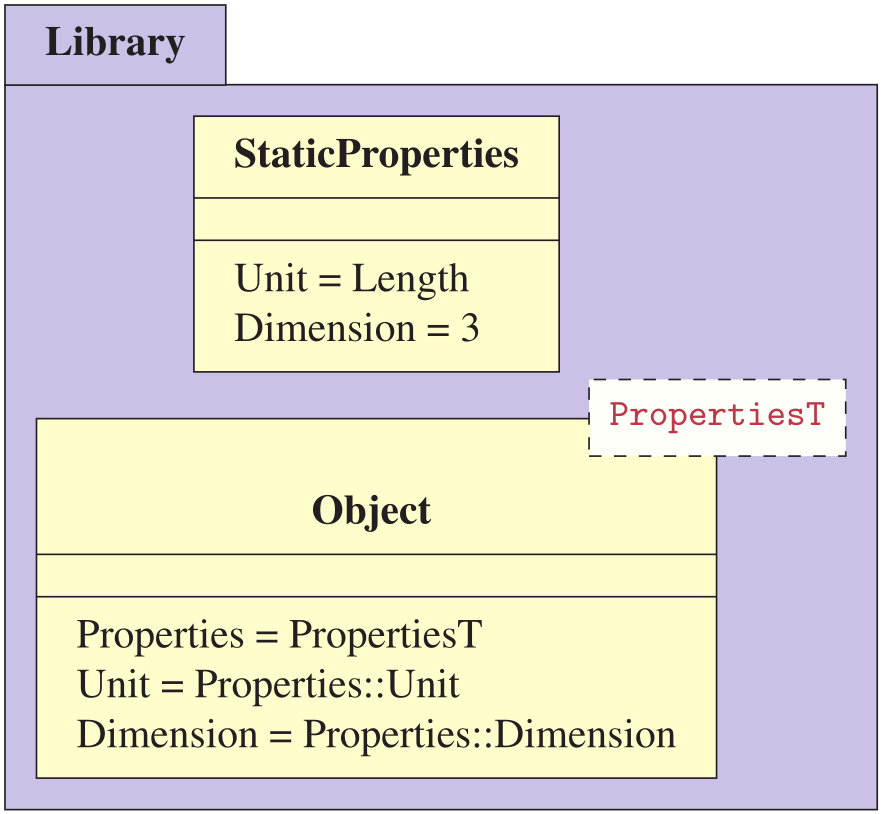
Static properties can be utilized to hold compile-time types or sizes such as an object's spatial dimension or base unit type. These are properties which are changed for instance to increase computational precision (e.g. long double or integer over floats), or to specify the dimension of an embedding space (e.g. two-dimensional, R2, instead of three-dimensional, R3). Such internal properties can be defined using static constant expressions or using type definitions as part of non-intrusive inheritance (is-a relationship), or as internal aggregated type definitions (is-a or has-a relationship).

|
Static properties are not part of an instantiated object by definition, but can be stored if needed. As such, this mechanism is powerful and inflicts no run-time penalty.

|
However, such properties are not aggregated through inheritance and must therefore be explicitly defined, as follows:
// Properties
struct StaticProperties {
using Unit = int;
static constexpr auto Dimension = 3ul; };
// Object
template ⟨typename Props_T⟩
struct Object {
using Unit = typename Props_T::Unit;
static constexpr auto Dimension = Props_T::Dimension; };
// Object instantiation
Object⟨StaticProperties⟩ object;
Transitive constructors and member functions
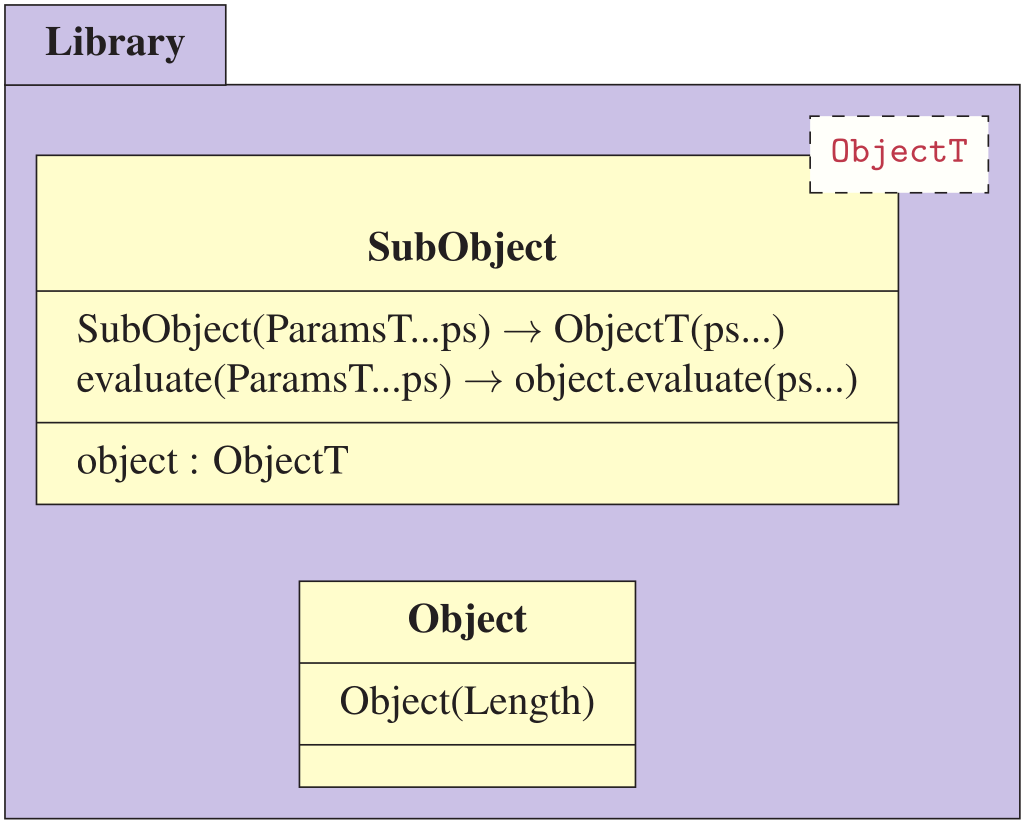
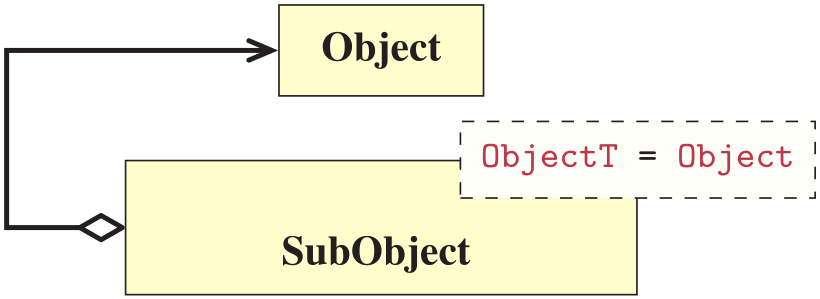
When utilizing a non-intrusive inheritance model we need a mechanism to transitively aggregate the future constructors of a class-type we do no yet know exists.
|
This can be achieved using a combination of templated constructors and variadic templates with perfect forwarding.

|
Let us exemplify it through an internal sub-object construction with a has-a relationship, as such:
template ⟨typename SubObj_T⟩
struct Object {
SubObj_T sub;
template ⟨typename... Ts⟩ Object(Ts&&... ts)
: sub(std::forward⟨Ts⟩(ts)...){}
};
struct A {
explicit A(float f) {}
explicit A(std::array⟨int,3⟩ i) {}
};
auto obj_one Object⟨A⟩(2.3f);
auto obj_two Object⟨A⟩({1,2,3});
Simplifying API through type definition
Finally, it is useful to simplify an API without introducing new types. This can be achieved by using type definition via the using directive. Contrary to the pre-C++11 standard's typedef directive, using directives can be templated.
Consider this API for a parametric object
template ⟨size_t PSpaceDim, size_t EmbedDim⟩
struct Object;
template ⟨size_t EmbedDim⟩
using Curve = Object⟨1ul,EmbedDim⟩;
template ⟨size_t EmbedDim⟩
using Surface = Object⟨2ul,EmbedDim⟩;
An Example Toy library
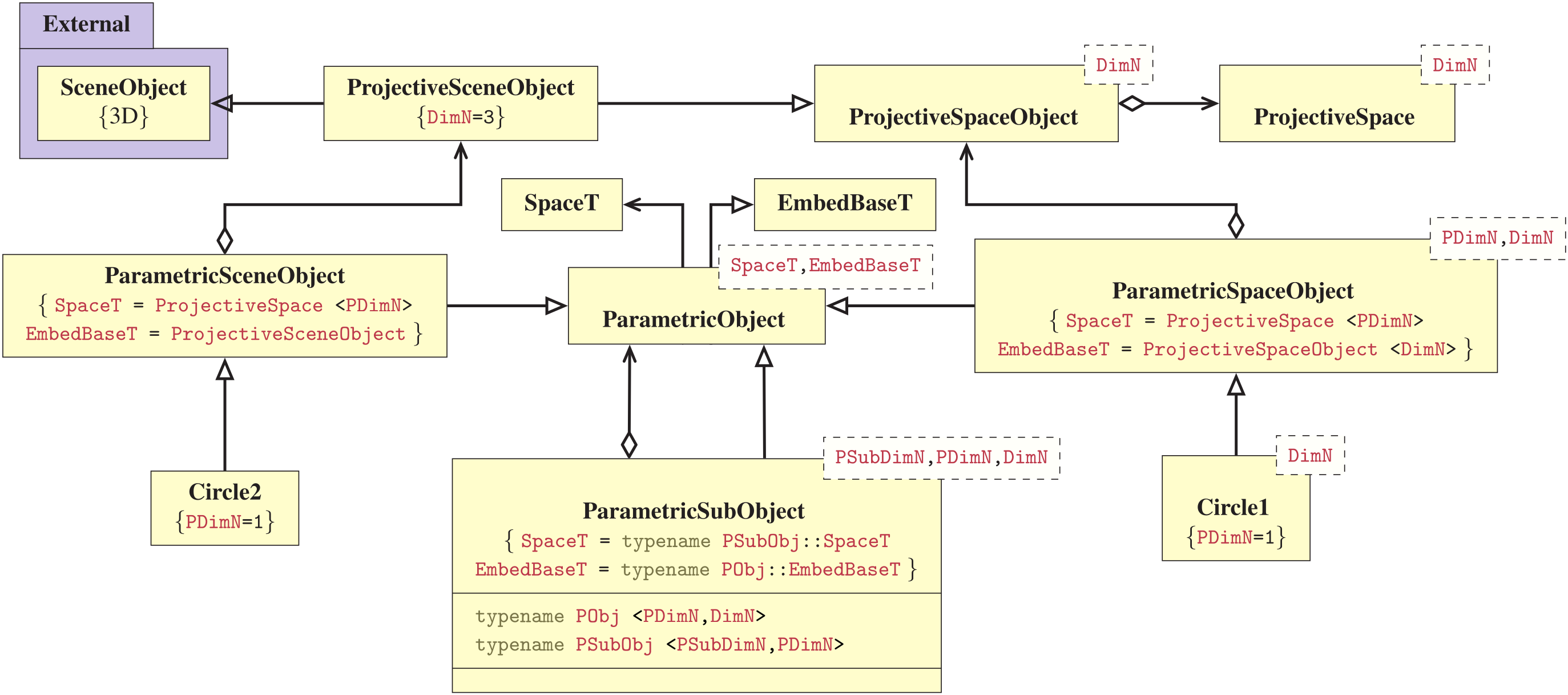
|
- Projective space
- Parametric object
- Parametric sub-object
- User-space API
- Usage
Projective space
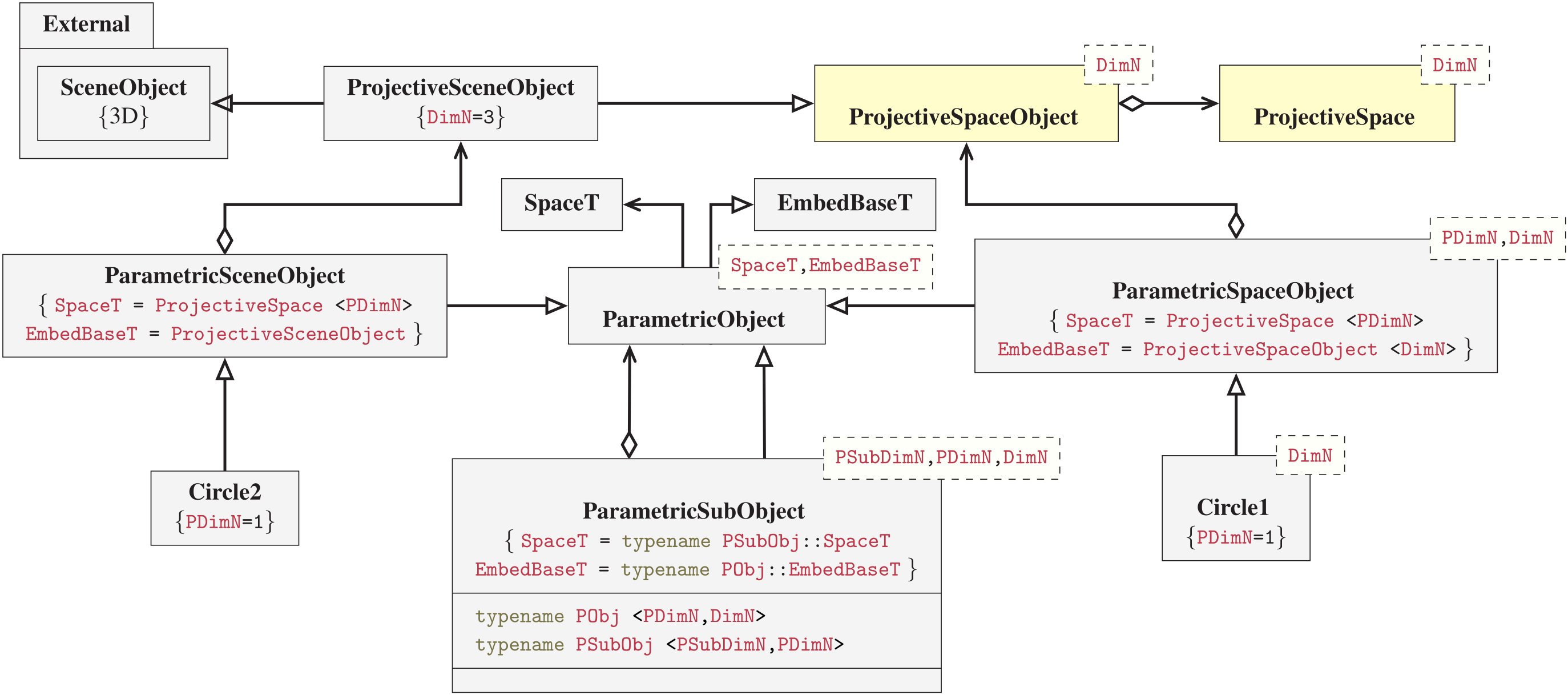
|
The projective space is common when working with visual parametric modeling. It is an affine mathematical space (see e.g. literature on differential- or Riemannian geometry), consisting of points and vectors with respect to a perspective projection such that parallel lines end up in a point at infinity, i.e., the horizon. The projective space meta-data description consists of its affine space containers for points and vectors in addition to a numerical unit data type and a spatial dimension. The space is usually represented as a frame in the shape of a homogeneous matrix.

|
We model the meta-information of this mathematical space statically by using an information only structure:
template ⟨typename Unit_T, size_t Dim_T⟩
struct ProjectiveSpace {
static constexpr auto Dim = Dim_T; // Space dimension
using Unit = Unit_T; // Storage unit type
using Point = Vector⟨Unit, Dim⟩; // Affine space data types
using Vector = Vector⟨Unit, Dim⟩;
using Frame = Matrix⟨Unit, Dim⟩;
};
template ⟨typename EmbedSpace_T⟩
struct ProjectiveSpaceObject {
using EmbedSpace = EmbedSpace_T; // Projective space
using Unit = typename EmbedSpace::Unit; // Type aggregation
/* ... */
Frame frame = {/* identity */}; // Affine space data structure
void translate( Vector ) { /*math*/ }; // Affine operations
/* ... */
};
Parametric objects
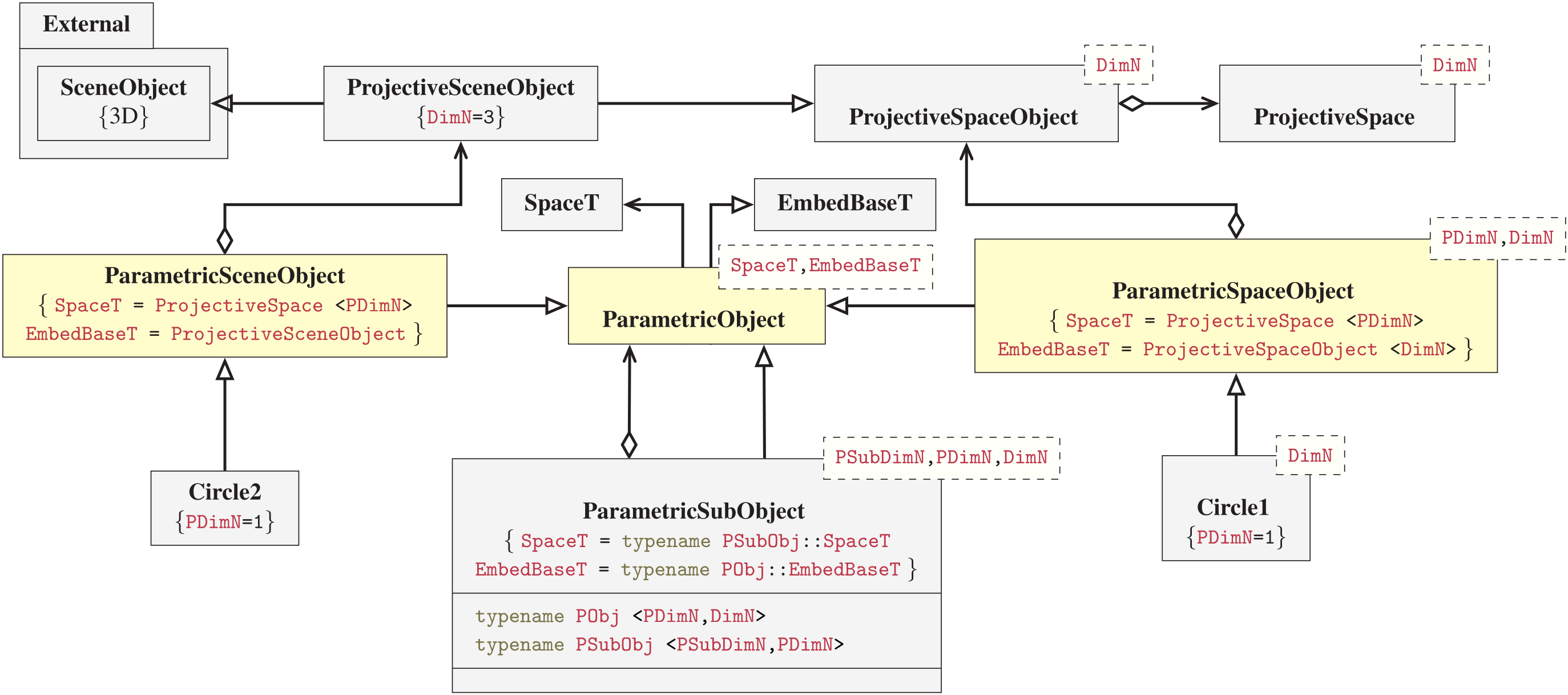
|
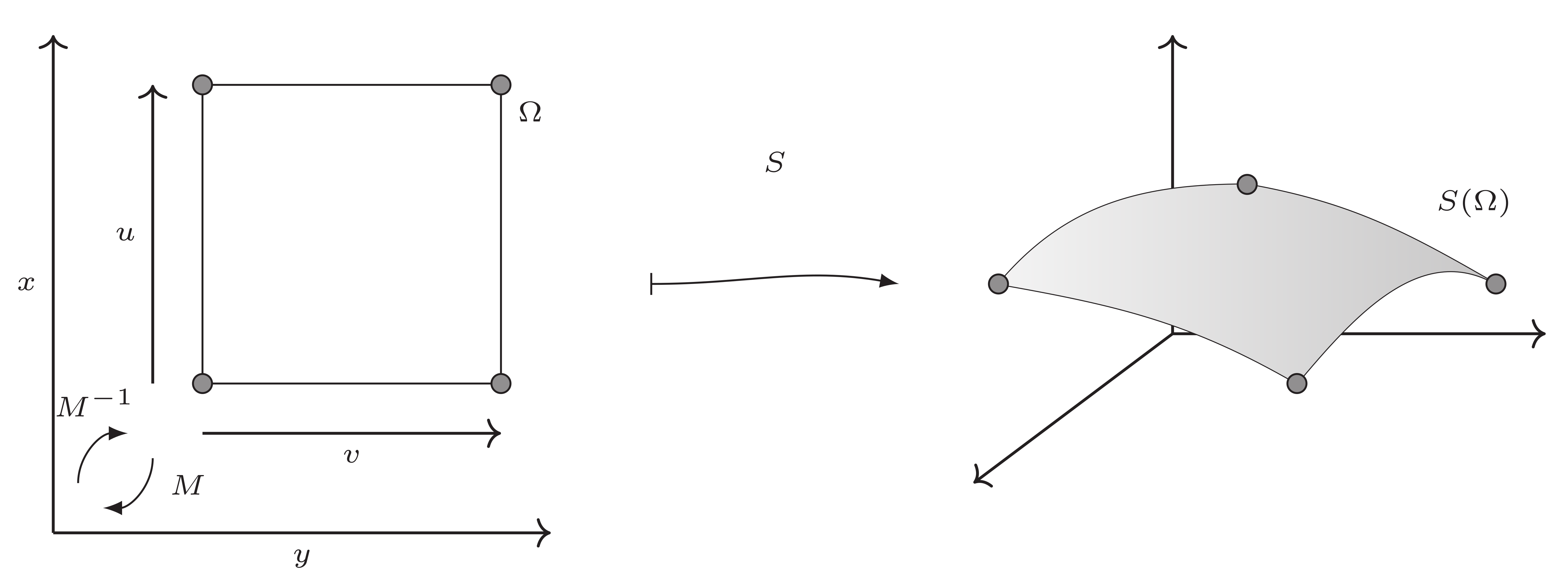
A parametric object is a user defined type describing a differential mapping from an n-dimensional parameter space into a m-dimensional embed space, under certain restrictions.
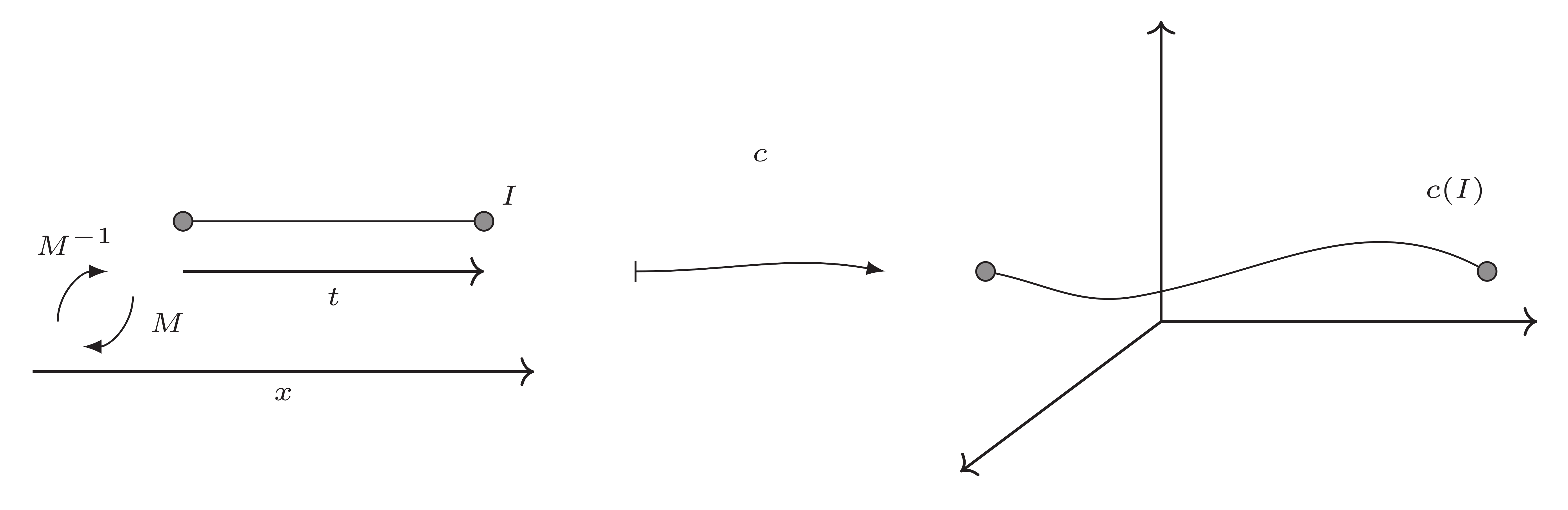
|
|
Object implementation driver (conceptual base class)
Let us begin by constructing a conceptual "base class". However this will be modeled using the principles of non-intrusive inheritance, where the parametric object base class implementation inherits a templated kernel type, Kernel_T, realizing the actual parametric object.

|
template ⟨typename Kernel_T⟩
struct ParametricObjectImpl : Kernel_T {
// Context
using Kernel = Kernel_T;
// Embed Space
using EmbedSpaceObj = typename Kernel::EmbedSpaceObj;
using EmbedSpace = typename Kernel::EmbedSpace;
using Unit = typename Kernel::Unit;
/* ... */
// Parametric space
using PSpace = typename Kernel::PSpace;
using PSpaceUnit = typename Kernel::PSpaceUnit;
/* ... */
auto evaluateParent(PSpacePoint par) {
return frame * evaluate(par); }
/* ... */
template ⟨typename... Ts⟩
explicit ParametricObjectImpl(Ts&&... ts)
: Kernel(std::forward⟨Ts⟩(ts)...) { }
}; // END ParametricObjectImpl
Parametric object kernels
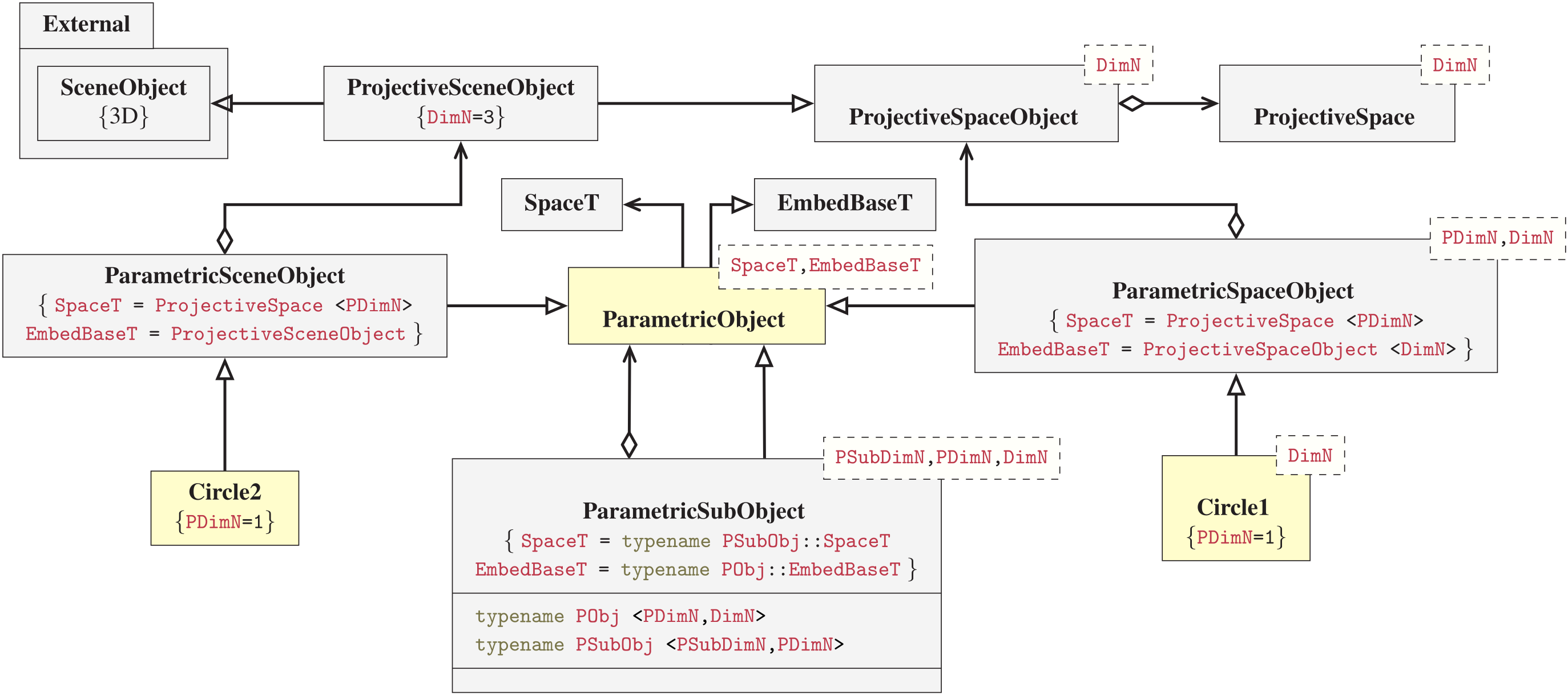
|
To realize a parametric object, such as a circle or a torus, we construct parametric object kernels.
Parametric circle kernel
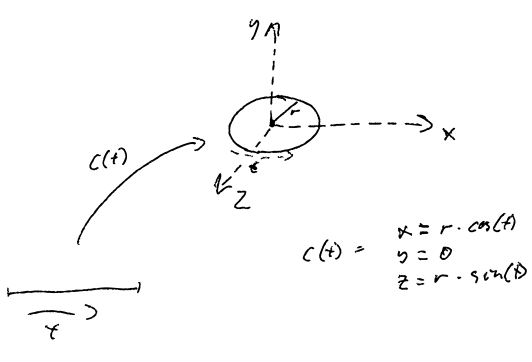


|
As an example, the parametric object kernel of a circle, CircleKernel, is constructed as a user defined type inheriting the projective space object as a template type, EmbedSpaceObj_T. Then as with the parametric object itself we use aggregated properties to inherit the static types. Additionally we define equivalent projective space types for the parameter space itself and extra utility types, prefixed PSpace. This, in fact, represents boilerplate code for any parametric curve.
template ⟨typename EmbedSpaceObj_T⟩
struct CircleKernel
: EmbedSpaceObj_T {
// Embed Space
using EmbedSpaceObj= EmbedSpaceObj_T;
using EmbedSpace = typename EmbedSpaceObj::EmbedSpace;
/* ... */
// PSpace
using PSpace = space::ProjectiveSpace⟨1ul,Unit⟩;
using PSpaceUnit = typename PSpace::Unit;
static constexpr auto PSpaceDim = PSpace::Dim;
/* ... */
// Utility
using PSpaceBoolArray = array⟨bool, PSpaceDim⟩;
using PSpaceSizeArray = array⟨size_t, PSpaceDim⟩;
// Member: radius
Unit r;
// Transitive constructor
template ⟨typename... Ts⟩
explicit CircleKernel(Unit radius = 3, Ts&&... ts)
: Base(std::forward⟨Ts⟩(ts)...), r{radius} {}
// Semantic polymorphic functions
auto evaluate(PSpacePoint par) const {
const auto& [t] = par;
const auto x = r * std::cos(t);
const auto y = r * std::sin(t);
if constexpr (Dim == 2) return Point{x, y}; // 2D
else if constexpr (Dim == 3) return Point{x, y, 0}; // 3D
}
PSpaceBoolArray isClosed() const { return {true}; }
PSpacePoint startParameter() const { return {0}; }
PSpacePoint endParameter() const { return {2*M_PI}; }
}; // END CircleKernel
Parametric torus kernel
Let us also see what the equivalent two-dimensional torus would look like.
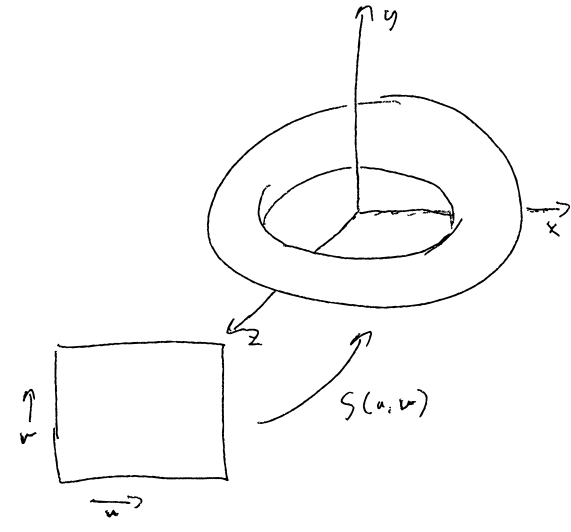

|
template ⟨typename EmbedSpaceObj_T⟩
struct TorusKernel
: EmbedSpaceObj_T {
// Embed Space
using EmbedSpaceObj= EmbedSpaceObj_T;
using EmbedSpace = typename EmbedSpaceObj::EmbedSpace;
/* ... */
// PSpace
using PSpace = space::ProjectiveSpace⟨2ul,Unit⟩;
using PSpaceUnit = typename PSpace::Unit;
static constexpr auto PSpaceDim = PSpace::Dim;
/* ... */
// Utility
using PSpaceBoolArray = array⟨bool, PSpaceDim⟩;
using PSpaceSizeArray = array⟨size_t, PSpaceDim⟩;
// Members
Unit wr; // Wheel radius
Unit tr1; // Tube radius 1
Unit tr2; // Tube radius 2
// Transitive constructor
template ⟨typename... Ts⟩
explicit TorusKernel(Unit wheelrad = 3, Unit tuberad1 = 1,
Unit tuberad2 = 1, Ts&&... ts)
: Base(std::forward⟨Ts⟩(ts)...), wr{wheelrad}, tr1{tuberad1}, tr2{tuberad2} {}
// Semantic polymorphic functions
auto evaluate(PSpacePoint par) const {
const auto& [u,v] = par;
const auto x = std::cos(u) * (tr1 * std::sin(v) + wr);
const auto y = std::sin(u) * (tr1 * std::sin(v) + wr);
const auto z = std::sin(v) * tr2;
// Embeded in 3D projective space
if constexpr (Dim == 3) return Point{x,y,z};
}
PSpaceBoolArray isClosed() const { return {true, true}; }
PSpacePoint startParameter() const { return {0, 0}; }
PSpacePoint endParameter() const { return {2 * M_PI, 2 * M_PI}; }
}; // END TorusKernel
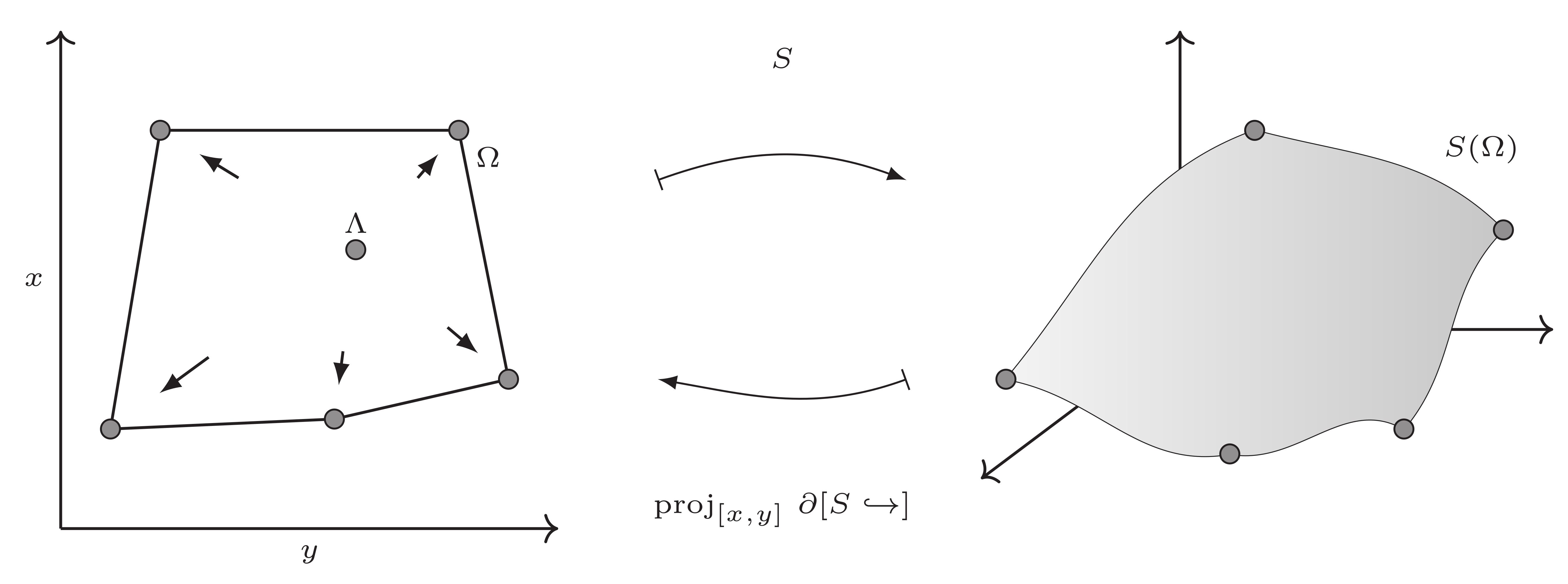
Parametric sub-object
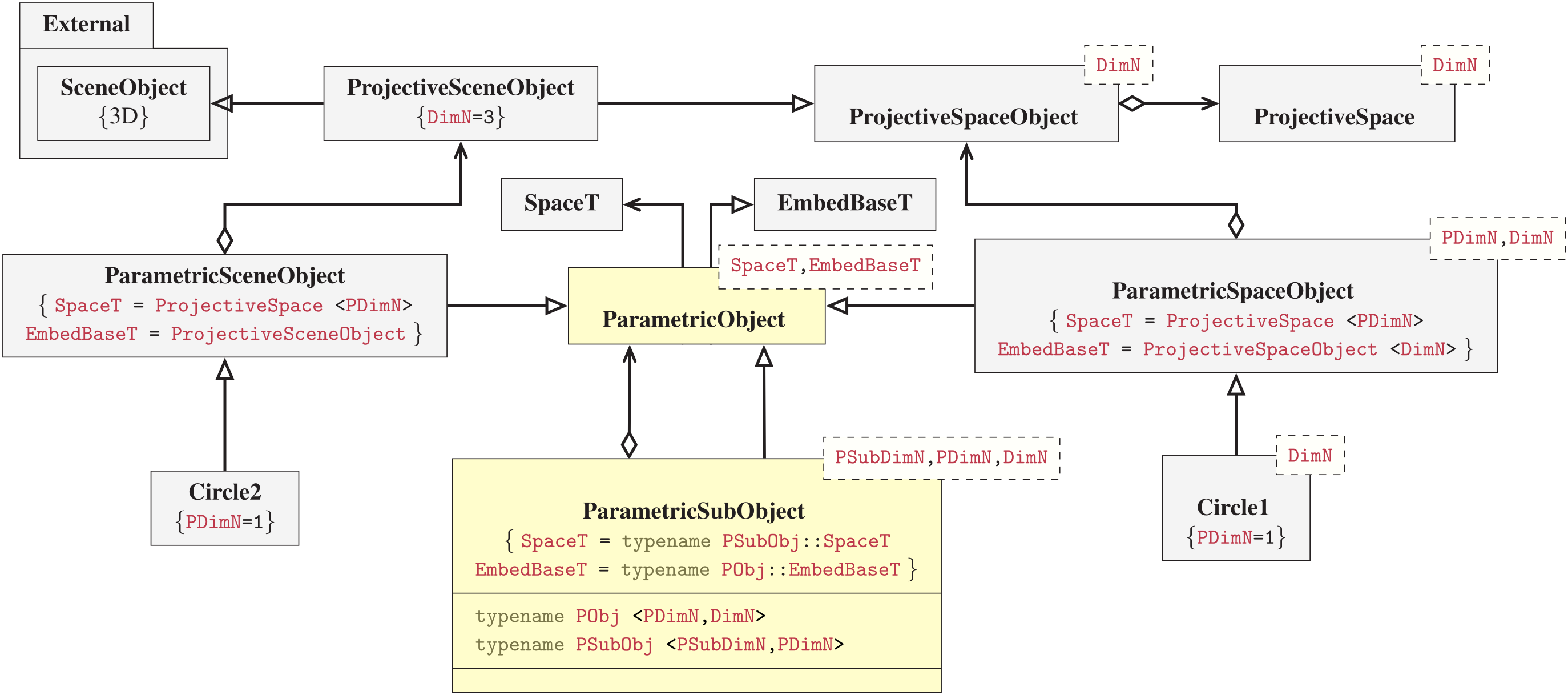
|
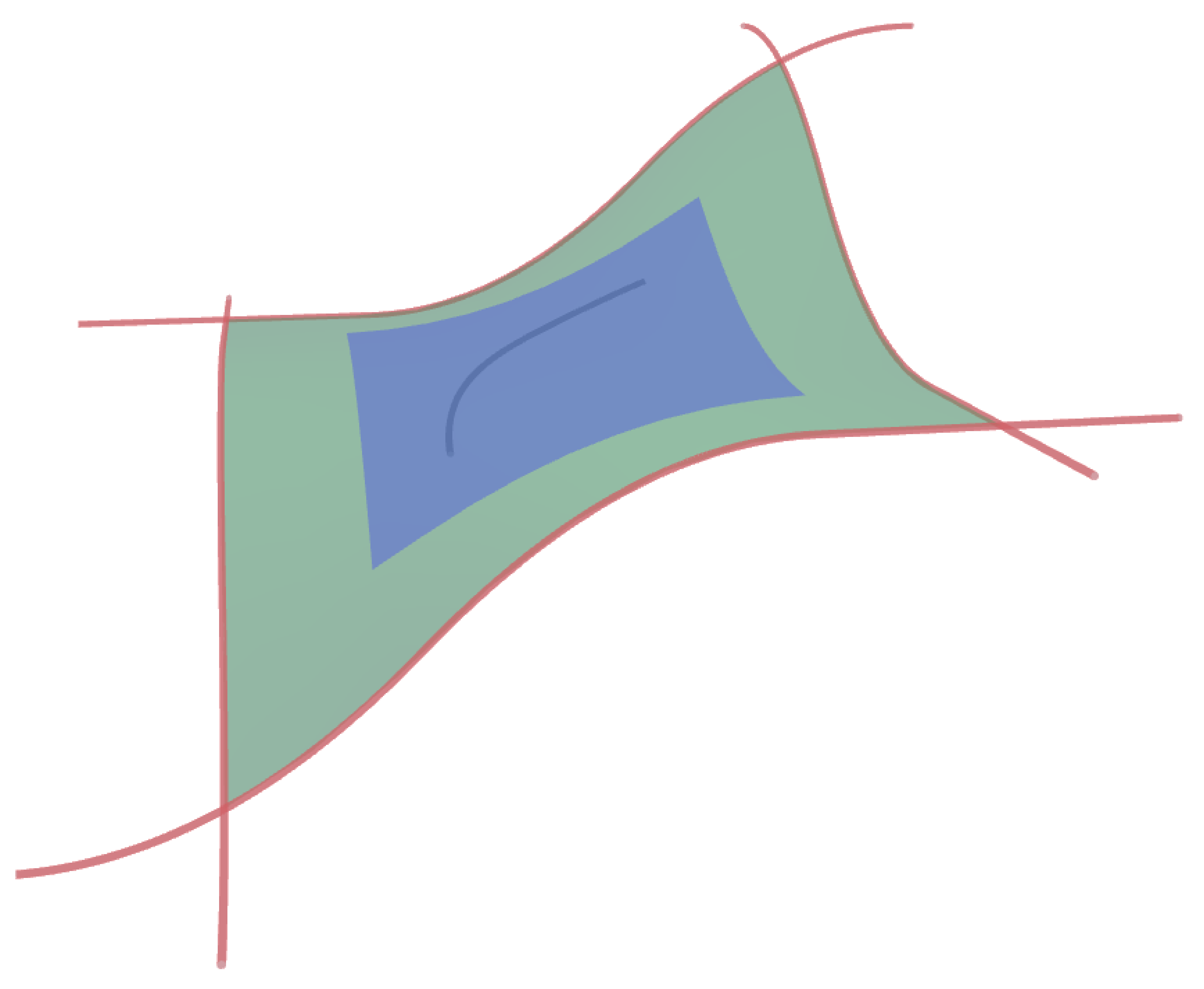
Contrary to the basic parametric object, a sub-object kernel is defined by a parametric object which is embedded in the parameter space of another parametric object. This can be achieved by defining the kernel and implementation of the sub-object slightly different to the parametric object type itself. However, as an invariant to achieve sub-object chaining, the internal type-definitions should be kept identical to the ones of the parametric object.

|
Parametric sub-object kernels
The kernel is defined from three types; the subbed parametric object, ParametricObject_T, a parametric object embedded in that parametric object's parametric space, PSpaceObject_T, and an embed space object, EmbedSpaceObject_T, which usually is the same as the embed space of the sub-object. This gives us a parametric object with three distinct spaces: the parametric space of the sub-object, PSpace, the parametric space of the parametric object, ParametricObject_PSpace, and the embed space of the parametric object, EmbedSpace. The fourth space, the embed space of the sub-object, is redundant as it would be the same space as the parametrics space of the parametric object, i.e.: PSpace.
template ⟨typename PSpaceObject_T, typename ParametricObject_T,
typename EmbedSpaceObject_T⟩
struct CurveInSurfaceKernel : EmbedSpaceObject_T {
using PSpaceObject = PSpaceObject_T; // Context
using ParametricObject = ParametricObject_T;
using EmbedSpaceObject = EmbedSpaceObject_T;
using EmbedSpace = typename EmbedSpaceObject::EmbedSpace;
using PSpace = typename PSpaceObject::PSpace;
using ParametricObject_PSpace = typename ParametricObject::PSpace;
using Unit = typename EmbedSpace::Unit;
/* ... */
Continuing, the sub-object's data members, constructor and polymorphic parametric object methods are defined as follows.
// Members
PSpaceObject pspace_object;
ParametricObject* parametric_object;
// Transitive constructor
template ⟨typename... Ts⟩
explicit SubCurveKernel(ParametricObject* obj, Ts&&... ts)
: Base(), pspace_object(std::forward⟨Ts⟩(ts)...),
parametric_object{obj} {} };
// Semantic polymorphic functions
auto evaluate(PSpacePoint par) const
{
const auto pspace_res = pspace_object.evaluate(par);
const auto parametric_object_res =
parametric_object->evaluate(pspace_res);
return parametric_object_res;
}
auto isClosed() const { return pspace_object.isClosed(); }
/* ... */
}; // END CurveInSurfaceKernel
Sub-object implementation driver (conceptual base class)
The conceptual base class type for the parametric sub-object type is just a small variation with respect to the the parametric object. Types are aggregated from the sub-object-in-object kernel, which transitively calls the right constructor combination. Again, it is important that it retains the same type definition interface as the ParametricObjectImpl such that it also can be used in sub-object chaining.
template ⟨typename Kernel_T⟩
struct ParametricSubObjectImpl
: ParametricObjectImpl⟨Kernel_T⟩ {
// Context
using Kernel = Kernel_T;
using PSpaceObject = typename Kernel::PSpaceObject;
using ParametricObject = typename Kernel::ParametricObject;
using EmbedSpaceObject = typename Kernel::EmbedSpaceObject;
// Aggregated types
using PSpace = typename Kernel::PSpace;
using EmbedSpace = typename EmbedSpaceObject::EmbedSpace;
using ParametricObject_PSpace =
typename Kernel::ParametricObject_PSpace;
// Delete default constructor
ParametricSubObjectImpl() = delete;
// Transitive Constructor
template ⟨typename... Ts⟩
explicit ParametricSubObjectImpl(ParametricObject* obj,
Ts&&... ts)
: Base(obj, std::forward⟨Ts⟩(ts)...) {}
}; // END ParametricSubObjectImpl
User-Space API
Finally, let us design a usable API. C++ template code naturally results in low readability API's, however, as discussed in beginning, this can be mended utilizing template using type-definitions:
// ParametricObject
template ⟨template ⟨typename⟩ typename Kernel_T,
typename EmbedSpaceObject_T⟩
using ParametricObject
= ParametricObjectImpl⟨Kernel_T⟨EmbedSpaceObject_T⟩⟩;
// ParametricSubObject
template ⟨template ⟨typename⟩ typename PSpaceKernel_T,
template ⟨typename, typename, typename⟩
typename Kernel_T,
typename ParametricObject_T⟩
using ParametricSubObject =
ParametricSubObjectImpl⟨Kernel_T⟨
ParametricObjectImpl⟨PSpaceKernel_T⟨ProjectiveSpaceObject⟨
typename ParametricObject_T::PSpace⟩⟩⟩,
ParametricObject_T,
ProjectiveSpaceObject⟨
typename ParametricObject_T::EmbedSpace⟩⟩⟩;
Object instantiation and usage
Using the AIP we can create instances of our objects.
// Define an embed-space - 3D
using ProjSpace = ProjectiveSpace⟨double,3ul⟩;
using ProjSpaceObj = ProjectiveSpaceObject⟨ProjSpace⟩;
// Define object types with our building blocks
using Circle = ParametricObject⟨CircleKernel, ProjSpaceObj⟩;
using Torus = ParametricObject⟨TorusKernel, ProjSpaceObj⟩;
// Create Objects
auto circle = Circle();
auto torus = Torus();
using SubCircle = ParametricSubObject⟨CircleKernel, SubCurveKernel, Torus⟩;
using SCUnit = SubCircle::Unit;
using SCPVector = SubCircle::PSpace::Vector;
using SCVector = SubCircle::Vector;
SCUnit radius{.5f};
auto subcurve = SubCircle(&torus, radius);
// Translate the torus
torus.wr += 0.5f;
// OR; subcurve.parametric_object->wr += 0.5f;
// Translate the embedded circle in the parametric space of the torus.
SCPVector offset{ M_PI, M_PI };
subcurve.pspace_object.translate(offset);
// Translate the circle in the resulting embedded space
SCVector tr { 1.f, 1.f, 1.f };
subcurve.translate(tr);
// Evaluate the torus
auto res_torus = torus.evaulate(); // quivalent to :
// OR; auto res_torus = subcurve.parametric_object->evaulate();
// Evaluate the circle in the torus' parametric space
auto res_pcircle = subcurve.pspace_object.evaulate();
// Evaluate the circle in the resulting embedded space
auto res_subcircle = subcurve.evaulate();
Complex construction examples (from GMlib2)
Sub-object chaining - Line in Plane in Torus
We can create sub-sub-objects by chainging them together.
// Space
using ProjSpace = ProjectiveSpace⟨double,3ul⟩;
using ProjSpaceObj = ProjectiveSpaceObject⟨ProjSpace⟩;
// Types
using Torus = ParametricObject⟨TorusKernel, ProjSpaceObj⟩;
using PlaneInTorus = ParametricSubObject⟨PlaneKernel, SubSurfaceKernel, Torus⟩;
using LineInPlaneInTorus = ParametricSubObject⟨LineKernel, SubCurveKernel, PlaneInTorus⟩;
// Objects
auto torus = Torus();
auto sub_plane = PlaneInTorus( &torus, /* plane params */);
auto sub_line = LineInPlaneInTorus( &sub_plane, /* line params */);
As showed in the beginning of the article, in this example we see a Line (curve) embedded in a Plane (surface) embedded in a Torus (surface).

|
Coons' construction from sub-objects
We can also use this construction technique to build more complex constructions. The example below shows a Coons' surface constructed from sub-curves.
// Space
using ProjSpace = ProjectiveSpace⟨double,3ul⟩;
using ProjSpaceObj = ProjectiveSpaceObject⟨ProjSpace⟩;
// Object Types
using HermiteCurve = ParametricObject⟨HermiteCurveKernel, ProjSpaceObj⟩;
using Coons = ParametricObject⟨CoonsKernel, ProjSpaceObj⟩;
// Sub-Object Types
using LineInHermiteCurve = ParametricSubObject⟨LineKernel, SubCurveKernel, HermiteCurve⟩;
using PlaneInCoons = ParametricSubObject⟨PlaneKernel, SubSurfaceKernel, Coons⟩;
using LineInPlaneInCoons = ParametricSubObject⟨LineKernel, SubCurveKernel, PlaneInCoons⟩;
// Coons' boundary objects
auto coons_bounds = std::array⟨HermiteCurve,4⟩ { /* aggregate initialization */ };
auto coons_subbounds = std::array⟨LineInHermiteCurve,4⟩;
std::ranges::transform( coons_bounds, coons_subbounds,
[]() { /* initialize sub-curves */} );
// Coons' surface
auto coons = Coons( /* coons_subbounds */ );
// Coons' sub-objects
auto sub_plane = PlaneInCoons( &coons, /* params */);
auto sub_line = LineInPlaneInCoons( &sub_plane, /* params */);
Inside the Coons' patch there is a sub-plane, which again has an embedded sub Hermite curve.
|
Sub polygons
The example below shows a sub-polygon surface on a polygon GB patch.
// Space
using ProjSpace = ProjectiveSpace⟨double,3ul⟩;
using ProjSpaceObj = ProjectiveSpaceObject⟨ProjSpace⟩;
// Types
using GBPatch = ParametricObject⟨GBPatchKernel, ProjectiveSpaceObject⟩;
using PolygonInGBPatch = ParametricObject⟨PolygonKernel, SubPolygonKernel, GBPatch⟩;
// Objects
auto gbpatch = GBPatch();
auto sub_patch = PolygonInGBPatch( &gbpatch, /* params */);

|
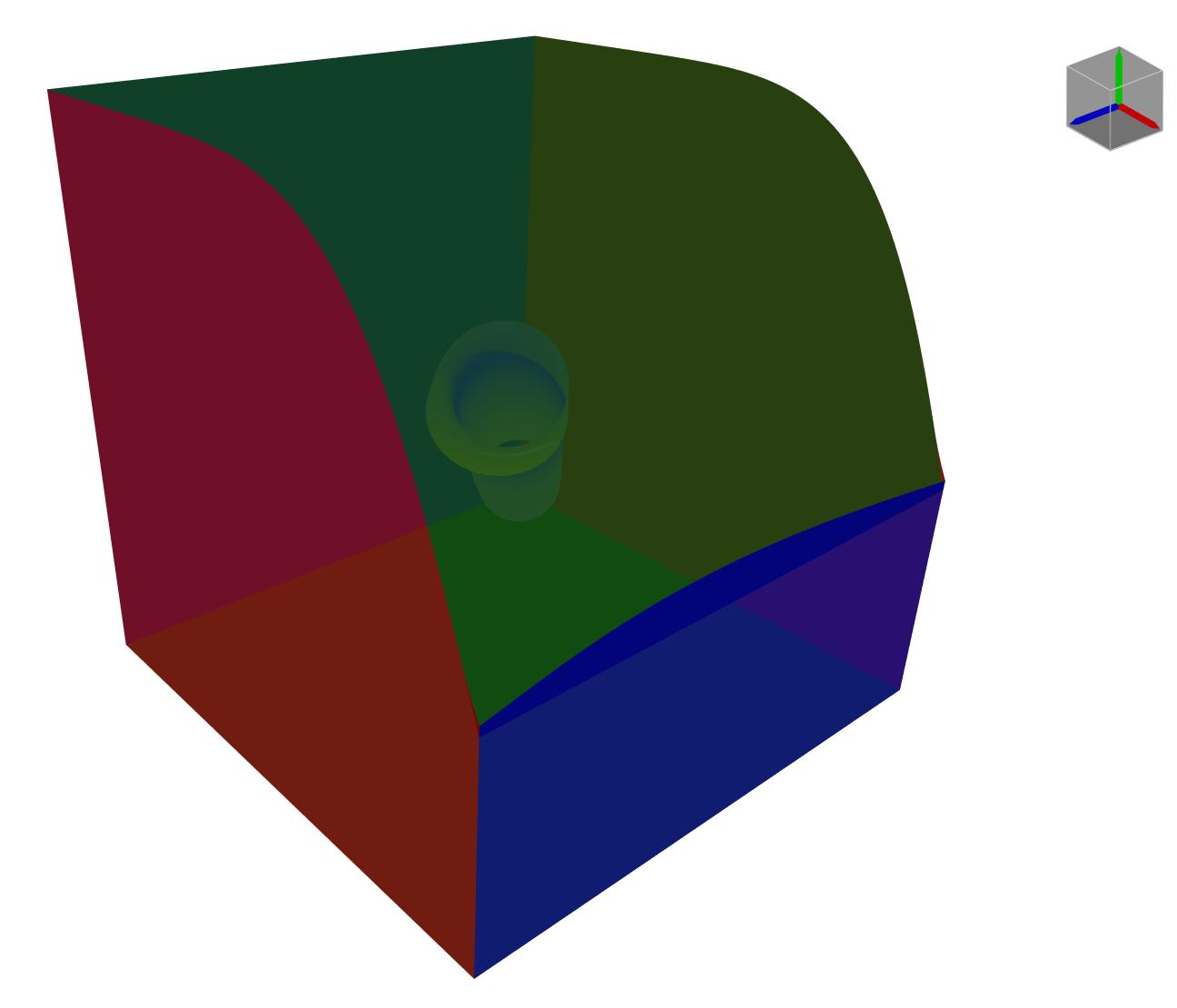
Volume embedded objects and volume visualization
As showed in the beginning of the article, here we se a cylinder embedded in the parametric space of a Beizer Volume.
// Space
using ProjSpace = ProjectiveSpace⟨double,3ul⟩;
using ProjSpaceObj = ProjectiveSpaceObject⟨ProjSpace⟩;
// Types
using BezierVolume = ParametricObject⟨BezierVolumeKernel, ProjectiveSpaceObject⟩;
using CylinderInVolume = ParametricObject⟨CylinderKernel, SubVolumeKernel, BezierVolume⟩;
using PlaneInVolume = ParametricObject⟨PlaneKernel, SubVolumeKernel, BezierVolume⟩;
// Objects
auto bezier_volume = BezierVolume();
auto sub_cylinder = CylinderInVolume( &bezier_volume, /* params */);
// Volume Visualization Objects
auto sub_plane_top = PlaneInVolume( &bezier_volume, /* params */);
auto sub_plane_bottom = PlaneInVolume( &bezier_volume, /* params */);
auto sub_plane_from = PlaneInVolume( &bezier_volume, /* params */);
auto sub_plane_back = PlaneInVolume( &bezier_volume, /* params */);
auto sub_plane_left = PlaneInVolume( &bezier_volume, /* params */);
auto sub_plane_right = PlaneInVolume( &bezier_volume, /* params */);


|



Resources
Links from the article
- The Toy Library @ \mi GitLab launch
Some of these objects you can check out in the museum.
- The museum read_more
GMlib2 has been developed as a live sandbox, and a C++ 20 rewrite was started after commit #5f42eb80, at commit #46236a95, which has left a lot of parametric objects without a port. These can be found by browsing the prior commit
- GMlib2 (c++17) parametric objects @ #5f42eb80 launch
- GMlib2 (c++20) parametric objects @ current launch
There are three runable demo applications for GMlib2 which contains parametric object implementations based upon these principles.